标签:
在函数调用中,通常我们都是在一个函数中调用另外一个函数,以此来完成其中的某部分功能。例如,我们在main()主函数中调用PowerSum()函数来计算两个数的平方和,而在PowerSum()函数中,又调用Power()函数和Add()函数来计算每个数的平方并将两个平方加和起来成为最终的结果。除此之外,在C++中还存在另外一种特殊的函数调用方式,那就是在一个函数内部调用它自己本身,这种方式也被称为函数的递归调用。
函数的递归调用,实际上是实现函数的一种特殊方式。当递归函数被调用的时候,会产生一个自己调用自己的循环,这个循环会不断地递归进行下去,直到最后一次函数调用在特殊条件下,也就是满足了递归的终止条件,不再继续调用自身而是返回某个具体的结果数据。这时,所有调用这个函数的上层函数会依次返回,直到我们最初对这个函数的调用返回,获得其结果数据。虽然函数的递归调用每次调用的都是自己,但是每次递归调用的条件,也即是函数参数,往往有所不同。正是调用条件的变化,才有可能使函数满足终止条件并返回一个具体的结果数据,不再继续递归地调用自身,这也即是递归调用的终点。
函数的递归调用虽然形式上比较复杂,但是它在处理那些可以把一个大问题分解成一个已知的结果与另一个类似的小问题,需要重复多次做相似的事情才能最终解决的问题时,因为函数的递归调用本身所表达的意义就是循环往复地做同一件事情,所以在处理这类问题上有着天然的优势。例如,我们要统计某个字符在目标字符串中出现的次数。通常,我们的思路是用for循环遍历整个字符数组,然后逐个字符地进行匹配统计。而如果采用递归函数的思路来解决这个问题,那么整个统计过程就变为:从目标字符串的开始位置查找这个字符,如果找到,那么字符出现的次数就成了已经找到的这一次加上在剩下的字符串中出现的次数,在程序中我们可以用“1 + CountChar(pos+1, c)”来表示,其中“1”表示已经找到的字符出现一次,而“CountChar(pos+1, c)”则代表了字符在剩下的字符串中出现的次数,加起来刚好就是字符在整个字符串中出现的次数。这里的“CountChar(pos+1, c)”就是在变更开始条件后对CountChar()函数的递归调用,进行第二次查找与统计。第二次查找也会进行类似的查找统计过程,如果找到则会第三次调用CountChar()函数继续向后继续查找统计。这个过程会不断地持续进行下去,直到最后满足递归的终止条件——查找到了字符串的结尾,再也找不到这个字符——为止。在这个过程中,有需要循环往复执行的相同动作——从字符串开始位置查找目标字符;有不同的开始条件——在字符串的不同位置开始查找;有终止条件——在字符串中再也找不到目标字符。有了这三个特征,我们就可以用函数的递归调用更轻松而自然地解决这个问题:
// countchar.cpp 统计一个字符串中某个字符出现的次数 #include <iostream> #include <cstring> // 引入字符查找函数strchr()所在的头文件 using namespace std; // 用函数的递归调用实现统计字符在字符串中出现的次数 int CountChar(const char* str,const char c) { // 从字符串str的开始位置查找字符c char* pos = strchr(str,c); // 如果strchr()函数的返回值为nullptr,则意味着 // 在字符串中再也找不到目标字符,递归的终止条件得到满足 // 则结束函数的递归调用,直接返回本次的查找结果0 if(nullptr == pos) { return 0; } // 如果没有达到终止条件,则将本次查找结果1统计在内, // 并在新的开始位置pos + 1开始下一次查找,实现函数的递归调用 return 1 + CountChar(pos + 1,c); } int main() { // 字符串 char str[] = "Thought is a seed"; char c = ‘h‘; // 目标字符 // 调用CountChar()函数进行统计 int nCount = CountChar(str,c); // 输出结果 cout<<"字符\‘"<<c<<"\‘在\""<<str<<"\"中出现了" <<nCount<<"次"<<endl; return 0; }
在执行的过程中,当CountChar()在主函数中第一次被调用时,第一个参数str指向的字符串是“Thought is a seed”,这时进入CountChar()函数执行,strchr()函数会在其中找到字符‘h’出现的位置并保存到字符指针pos中,此时尚不满足终止条件(nullprt == pos), 则执行“return 1 + CountChar(pos+1,c)”,将本次查找结果统计在内,并变更递归的开始条件为“pos+1”,让第二次递归调用CountChar()函数时参数str指向的字符串变为“ought is a seed”。在第二次进入CountChar()函数执行时,strchr()函数会找到字符‘h’第二次出现的位置,递归的终止条件依然无法得到满足,则继续将本次查找结果统计在内并修改开始条件,将CountChar()函数的str参数指向“t is a seed”,开始第三次递归调用。在第三次进入CountChar()函数执行时,strchr()函数在剩下的字符串中再也找不到目标字符,递归的终止条件得到满足,函数直接返回本次的查找统计结果0(return 0;),不再继续向下递归调用CountChar()函数,然后逐层向上返回,最终结束整个函数递归调用的过程,得到最终结果2,也就是目标字符在字符串中出现的次数。整个过程如下图5-8所示。
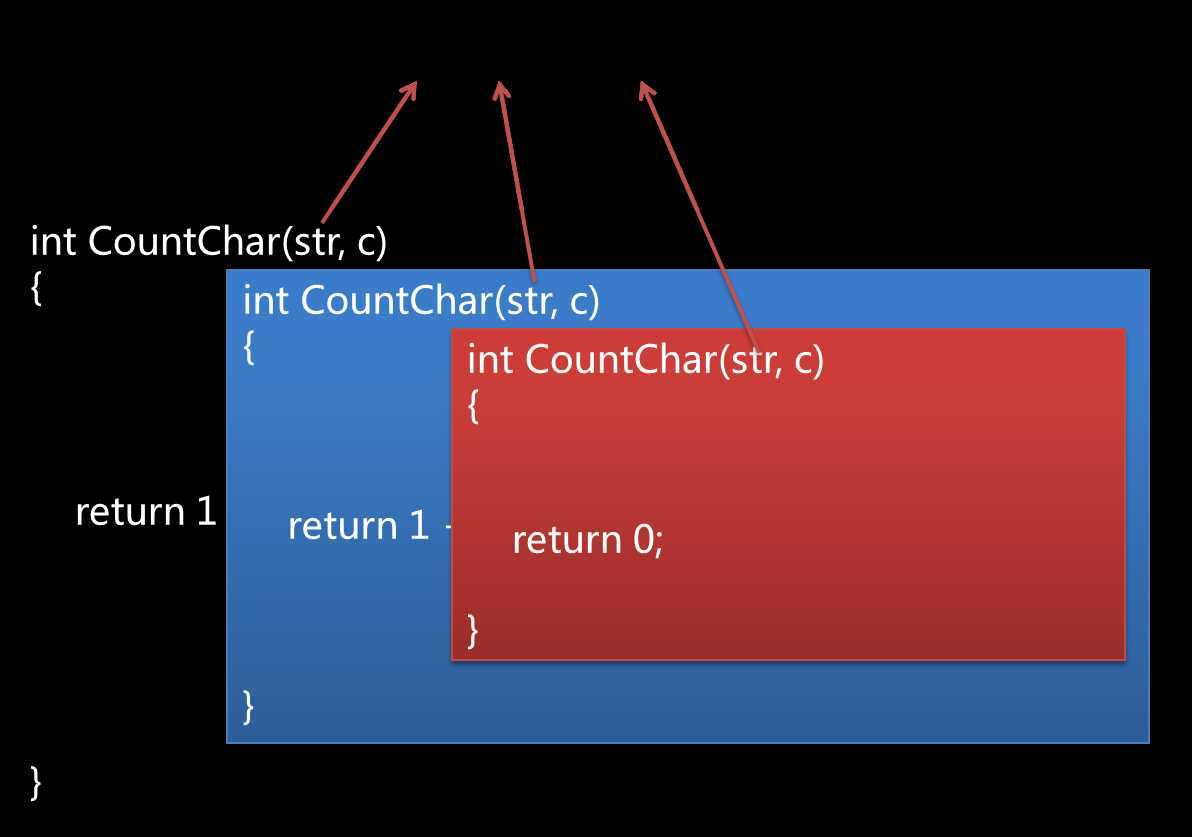
图5-8 CountChar()函数的递归调用过程
函数的递归调用,其实质就是将一个大问题不断地分解成多个相似的小问题,然后通过不断地细分,直到小问题被解决,才最终解决最开始的大问题。例如在这个例子中,我们开始的大问题是统计字符串中的目标字符的个数,然后这个大问题被分解为当前已经找到的目标字符数1和剩余字符串中的目标字符数CountChar(pos+1,c),而我们要计算剩余字符串中的目标字符数,又可以采用同样的策略进一步细分,直至剩余字符串中没有目标字符,无法继续细分为止。从这里我们也可以看到,函数的递归调用实际上是一个循环过程,我们必须确保函数能够达到它的递归终止条件,结束递归。例如,我们这里不断地调整查找的开始位置,让查找到最后再也无法找到目标字符而满足终止条件。否则,函数会无限地递归调用下去,最终形成一个无限循环而永远无法获得结果。这一点是我们在设计递归函数时尤其需要注意的。
函数的递归调用,是通过在一个函数中循环往复地调用它自身来完成的,从本质上讲,函数的递归调用其实是一种特殊形式的循环。所以,我们也可以将一个函数的递归调用改用循环结构来实现。例如,上面的CountChar()函数可以用循环结构改写为:
// 用循环结构实现统计字符在字符串中出现的次数 int CountChar(const char* str,const char c) { int nTotal = 0; // 记录字符出现次数 // 在字符串中查找字符,并对结果进行判断 // 如果strchr()返回nullptr,则表示查找完毕,循环结束 while(nullptr != (str = strchr(str,c))) { ++nTotal; // 将找到的字符统计在内 ++str; // 字符串往后移动,开始下一次循环 } return nTotal; }
这里我们不禁要问,既然函数的递归调用可以用循环结构来实现,而函数的递归调用又涉及到函数调用时的那些传递参数保护现场的幕后工作,性能比较低下,那么我们为什么还要使用函数的递归调用而不是直接使用效率更高的循环结构来解决问题呢?这是因为,面对某些特殊问题,我们很难用循环结构来解决。比如,从一个数组中找出连续和值最大的数据序列,如果采用循环结构,我们几乎无从下手,即使最后解决了但性能也是十分低下。而恰好这种问题又可以细分成多个类似的小问题,比如这里我们可以将数组分成左右两部分,那么和值最大的数据序列要么在左边部分,要么在右边部分,要么跨越两个部分。这样,这个问题就细分成了寻找左边部分、右边部分和跨越左右部分的和值最大序列的三个相似的小问题。而这三个小问题又可以进一步细化,直至最后可以轻松解决的最小问题。在这种情况下使用函数的递归调用来解决问题,更加符合我们人类的思考方式,问题解决起来更加容易,同时其性能也会优于循环结构的实现,做到了“又好又快”。解决这类可以不断细分的特殊问题,就是函数递归调用的用武之地。
你好,C++(27)在一个函数内部调用它自己本身 5.1.5 函数的递归调用
标签:
原文地址:http://www.cnblogs.com/nihaoCPP/p/4191327.html