标签:
《算法导论》中堆排序主要将其分为堆的性质、维护堆的性质、建堆、堆排序算法
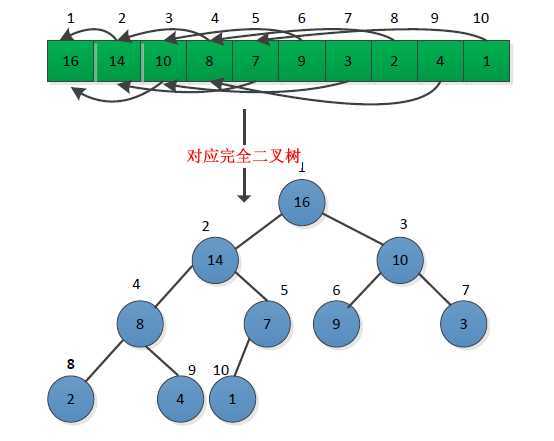
堆的性质:给定一个结点的下标i,很容易计算得到它的父结点、左孩子和右孩子的下标(伪代码):
PARENT(i) return i/2 LEFT(i) return 2i RIGHT(i) return 2i+1
这里针对下标从1开始的数组,然而实际上我们涉及的数组都是从0开始。为了改进上面的伪代码,可以使用移位来解决,其伪代码:
PARENT(i) return (i-1)>>1 LEFT(i) return ((i+1)<<1)-1 RIGHT(i) return (i+1)<<1
维护堆的性质(MAX-HEAPIFY):
MAX-HEAPIFY是用于维护最大堆性质的重要过程。他输入为一个数据A和一个下标i,在调用MAX-HEAPIFY的时候,假定根节点为LEFT(i)和RIGHT(i)的二叉树都是最大堆,但这时A[i]有可能小于其孩子,这样就违背了最大堆的性质。MAX-HEAPIFY通过让A[i]的值在最大堆中“逐级下降”,从而使得以下标i为根结点的子树重新遵循最大堆的性质。其伪代码如下所示:
MAX-HEAPIFY(A, i) l = LEFT(i); r = RIGHT(i); if l <= A.heap-size and A[l] > A[i] largest = largest else largest = i; if r <= A.heap-size and A[r] > A[largest] largest = r if largest != i exchangeA[i]withA[largest] MAX-HEAPIFY(A, largest)
用Java语言实现维护堆的性质:MAXHeapify.java
package heapsort; public class MaxHeapify { public void heapAdjust(int[] A, int i, int len){ int l = Left(i); int r = Right(i); int largest = i;//假设父节点值最大 if (l < len && A[l] > A[i]) {//左孩子值大于父节点值 largest = l; } if (r < len && A[r] > A[largest]) {//右孩子值大于父节点值 largest = r; } if (largest != i) { //exchange A[i]withA[largest] int tmp = A[i] ; A[i] = A[largest]; A[largest] = tmp; heapAdjust(A, largest, len); } } private int Right(int i) {//右孩子坐标 return ((i+1)<<1); // return 2*i+1; } private int Left(int i) {//左孩子坐标 return ((i+1)<<1)-1; // return 2*i; } }
测试维护堆的性质代码即:MaxHeapifyTest.java
package heapsort; public class MaxHeapifyTest { public static void main(String[] args) { int[] A ={16, 4, 10, 14, 7, 9, 3, 2, 8, 1}; // int[] A={5, 2, 4, 6, 1, 3, 2, 6}; MaxHeapify maxHeapify = new MaxHeapify(); maxHeapify.heapAdjust(A, 1, A.length); for (int i = 0; i < A.length; i++) { System.out.print(A[i]+" "); } } }
测试结果:
16 14 10 8 7 9 3 2 4 1
建堆(BUILD-MAX-HEAPIFY):
用自底向上的方法利用过程MAX-HEAPIFY把一个大小为n=A.length的数组A[1..n]转换为最大堆。通过一个证明:当用数组表示存储n个元素的堆时,叶节点下标分别为floor(n/2)+1,floor(n/2)+2,...,n。可知道,子数组A[floor(n/2)+1..n]中的元素都是树的叶结点。每个叶结点都可以看成只包含一个元素的堆。过程BUILD-MAX-HEAPIFY对树中的其他结点都调用一次MAX-HEAPIFY。其伪代码如下:
BUILD-MAX-HEAP(A) A.heap-size = A.length for i = floor(A.length/2) downto 1 MAX-HEAPIFY(A, i)
用Java语言实现BUILD-MAX-HEAPIFY功能即:BuildHeap.java
package heapsort; public class BuildHeap { public void buildMaxHeap(int[] A) { for (int i = A.length/2-1; i >= 0; i--) { MaxHeapify maxHeapify = new MaxHeapify(); maxHeapify.heapAdjust(A, i, A.length); } } }
测试建堆的功能即BuildHeapTest.java:
package heapsort; public class BuildHeapTest { public static void main(String[] args) { int[] A = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}; BuildHeap buildHeap = new BuildHeap(); buildHeap.buildMaxHeap(A); for (int i = 0; i < A.length; i++) { System.out.print(A[i]+" "); } } }
测试结果:
16 14 10 8 7 9 3 2 4 1
堆排序算法:
初始时候,堆排序算法利用BUILD-MAX-HEAP将输入数组A[1..n]建成最大堆,其中n=A.length。因为数组中的最大元素总在根结点A[1]中,通过把它与A[n]进行互换,我们可以让该元素放到正确的位置。这时候,如果我们从堆中去掉结点n(这一操作可以通过减少A.heap-size的值来实现),剩余的结点中,原来根的孩子结点仍然是最大堆,而新的根结点可能会违背最大队的性质。为了维护最大堆的性质,我们要做的是调用MAX-HEAPIFY(A, 1),从而在A[1..n-1]上构造一个新的最大堆。堆排序算法会不断重复这一过程,直到堆的大小从n-1降到2.
HEAPSORT(A) BUILD-MAX-HEAP(A) for i = A.length downto 2 exchange A[1] with A[i] A.heapsize = A.heapsize-1 MAX-HEAPIFY(A, 1)
注意:本段伪代码数组下标从1开始,要想实现该段伪代码时候,要将下标改为0开始。
用Java代码实现堆排序即HeapSort.java:
package heapsort; public class HeapSort { public HeapSort(int[] A) { BuildHeap buildHeap = new BuildHeap(); buildHeap.buildMaxHeap(A); for (int i = A.length-1; i > 0; i--) { //exchange A[1]withA[i] int tmp = A[0]; A[0] = A[i]; A[i] = tmp; //维护堆的性质 MaxHeapify maxHeapify = new MaxHeapify(); maxHeapify.heapAdjust(A, 0, i);//A[0]为根结点 } } }
测试堆排序算法即HeapSortTest.java:
package heapsort; public class HeapSortTest { public static void main(String[] args) { int[] A = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}; HeapSort heapSort = new HeapSort(A); for (int j = 0; j < A.length; j++) { System.out.print(A[j]+" "); } } }
测试结果:
1 2 3 4 7 8 9 10 14 16
标签:
原文地址:http://www.cnblogs.com/chuji1988/p/4205640.html