标签:
题意:给出两个排列,求出每个排列在全排列的排行,相加,模上n!(全排列个数)得出一个数k,求出排行为k的排列。
解法:首先要得出定位方法,即知道某个排列是第几个排列。比如 (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1), (2, 1, 0).
拿排列(1,2,0)来说,首位是1,前面有cnt=1个小于1的没被用过的数(0),所以它的排行要加上(cnt=1)*2!,第二位为2,因为1已经放了,所以小于2的只有0了,即cnt=1个,所以,排行又要加上(cnt=1)*1!,所以排行为3.
推出一般性结论:
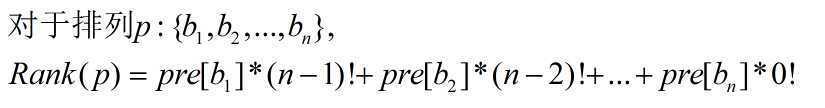
pre[i]表示小于 i 且没被占据的数的个数。我们可以用树状数组一边更新一边查询求得给出的两个排列的所有pre[]值,存到p数组:p1[i] = pre1[b1[i]],p2[i] = pre2[b2[i]]
然后Rank和为(p1[i]+p2[i])*(n-1)! + ... + (p1[n]+p2[n])*0! = p3[1]*(n-1)! + ... + p3[n]*0! ,但是得出的表达式可能不是规整的形式,这是我们需要检测一边,从后往前扫,如果p3[i] >= (n-i+1), 说明第 i 项已经超过 (n-i+1)*(n-i), 那么就应进位到(n-i+1)!, 即p3[i-1]+=1,依此类推,第1位的进位不再考虑。
最后得出规整的正确的p3[]序列,然后通过树状数组+二分在nlognlogn的复杂度将p3每位对应到结果排列的每位数上,即为上面求Rank(p)的反操作,不细讲了,想一想就知道了。
代码:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <string>
#include <vector>
#include <queue>
using namespace std;
#define N 200107
int p1[N],p2[N],p3[N],c[N];
int n;
int lowbit(int x) { return x&-x; }
void modify(int x,int val)
{
while(x <= n+10)
{
c[x] += val;
x += lowbit(x);
}
}
int getsum(int x)
{
int res = 0;
while(x > 0)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int main()
{
int i,j,x;
while(scanf("%d",&n)!=EOF)
{
memset(c,0,sizeof(c));
for(i=1;i<=n;i++) modify(i,1);
for(i=1;i<=n;i++)
{
scanf("%d",&x);
x++;
p1[i] = getsum(x-1);
modify(x,-1);
}
memset(c,0,sizeof(c));
for(i=1;i<=n;i++) modify(i,1);
for(i=1;i<=n;i++)
{
scanf("%d",&x);
x++;
p2[i] = getsum(x-1);
modify(x,-1);
}
memset(p3,0,sizeof(p3));
for(i=n;i>=1;i--)
{
p3[i] += p1[i]+p2[i];
if(p3[i] >= (n-i+1))
{
p3[i] = p3[i]-(n-i+1);
if(i != 1) p3[i-1]++;
}
}
memset(c,0,sizeof(c));
for(i=1;i<=n;i++) modify(i,1);
// for(i=1;i<=n;i++)
// cout<<p3[i]<<" ";
// cout<<endl;
for(i=1;i<=n;i++)
{
int low = 1, high = n;
while(low <= high)
{
int mid = (low+high)/2;
if(getsum(mid-1) > p3[i])
high = mid-1;
else if(getsum(mid-1) == p3[i] && getsum(mid)-getsum(mid-1) == 1)
high = mid-1;
else if(getsum(mid-1) == p3[i] && getsum(mid)-getsum(mid-1) < 1)
low = mid+1;
else if(getsum(mid-1) < p3[i])
low = mid+1;
}
modify(low,-1);
printf("%d ",low-1);
}
puts("");
}
return 0;
}
比赛中写的代码,没有最简化,有很多冗余和多此一举的地方。
Codeforces Round #285 (Div.1 B & Div.2 D) Misha and Permutations Summation --二分+树状数组
标签:
原文地址:http://www.cnblogs.com/whatbeg/p/4219667.html