Dijkstra算法

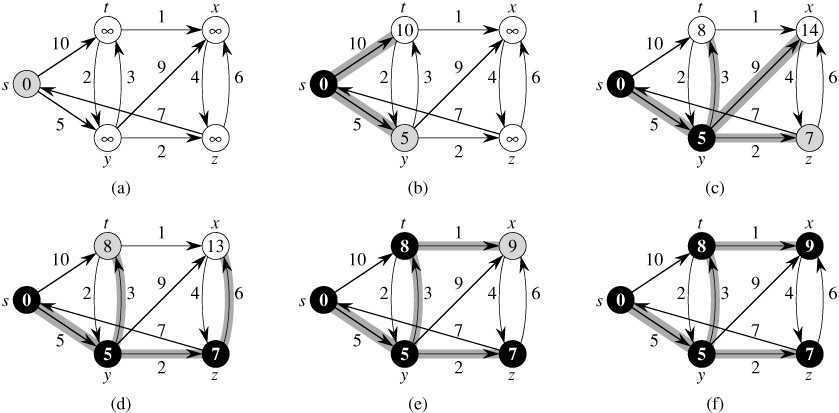
struct Vertice_comparator
{
    bool operator()(Vertice const * a, Vertice const * b)
    {
        return !!(a->distance > b->distance);
    }
};
typedef vector<Vertice*> Queue;

void Graph::dijkstra(int source_id)
{
    Vertice_comparator cmp = Vertice_comparator();
    if ((*this)[source_id] == NULL)
    {
        printf_s("找不到源节点%d\n", source_id);
        return;
    }
#pragma region 初始化
    Queue q = Queue();
    for (Node v : allVertices)
    {
        v.second->distance = v.first == source_id ? 0 : numeric_limits<int>::max();
        q.push_back(v.second);
    }
#pragma endregion 初始化
    while (!q.empty())
    {
        // 因为你要在队列外部改变Vertice*所指的内容
        // 而priority_queue又没开放重新建堆的接口
        // 所以用<algorithm>头文件里的make_heap建堆
        make_heap(q.begin(), q.end(), cmp);
        Vertice* u = q.front();
        cout << "当前结点 " <<u->id << endl;
        q.erase(q.begin()); // pop()
        for (Edge adj : u->adjacentVertices)
        {
            #pragma region 贪心
            if ((adj.target->distance) > (u->distance+adj.weight))
            {
                adj.target->distance = u->distance + adj.weight;
            }
            #pragma endregion 贪心
        }
    }
}