标签:
首先定义一个两个数对换的函数——swap

void swap(int *a1, int *a2) { int tmp; tmp = *a1; *a1 = *a2; *a2 = tmp; }
1 插入排序:有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序。
如图:
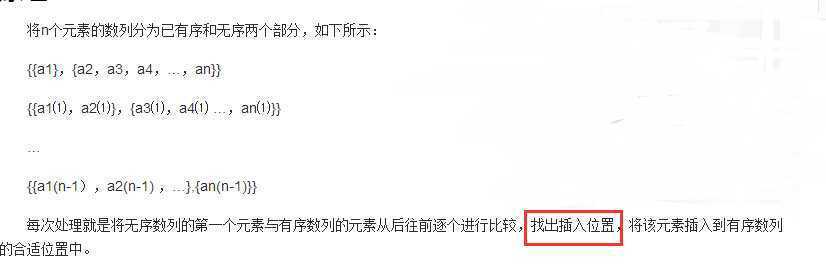
下面这个是我写的插入排序,不能算是真正意义上的插入排序。我的思想确实是把后面无序的第一个元素插入前面已经排好序的数组中,但是第11,12行的思想并不是找到合适的插入位置,而是逐个比较,无序的第一个元素和有序区的元素逐个交换。
1 void sorting(int *a, int n) 2 { 3 int i, j,key; 4 for (j = 1; j <n; j++) 5 { 6 key = j; 7 for (i = j - 1; i >= 0; i--) 8 { 9 if (a[i]>a[key]) 10 { 11 swap(&a[i], &a[key]); 12 key = i; 13 14 15 } 16 17 } 18 } 19 20 }
这是一个标准版本的插入排序:第9行表示如果有序区的元素大于key,则将该元素后移一位,直到到了有序区首位或是找到小于key的元素时,将key插入适当位置。
1 void sorting(int *a, int n) 2 { 3 int i, j,key; 4 for (j = 1; j <n; j++) 5 { 6 key = a[j]; 7 for (i = j; i >0&&a[i-1]>key; i--) 8 { 9 a[i] = a[i - 1]; 10 11 } 12 a[i] = key; 13 } 14 15 }
2 冒泡排序:它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。随着趟数的增多,每趟需要比较的次数逐渐减少。
1 void sorting(int *a, int n) 2 { 3 int i, j; 4 for (i = 0; i < n - 1; i++) 5 { 6 for (j = 1; j < n - i; j++) 7 { 8 if (a[j - 1]>a[j]) 9 { 10 swap(&a[j - 1], &a[j]); 11 } 12 } 13 } 14 }
3 选择排序:每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完
1 void sorting(int *a, int n) 2 { 3 int i, j,min; 4 for ( i = 0; i < n-1; i++) 5 { 6 min = i; 7 for ( j = i+1; j < n; j++) 8 { 9 if (a[min] > a[j]) 10 min = j; 11 } 12 swap(&a[i], &a[min]); 13 14 } 15 }
标签:
原文地址:http://www.cnblogs.com/Daringoo/p/4224976.html