标签:
原文:算法系列15天速成——第六天 五大经典查找【下】大家是否感觉到,树在数据结构中大行其道,什么领域都要沾一沾,碰一碰。
就拿我们前几天学过的排序就用到了堆和今天讲的”二叉排序树“,所以偏激的说,掌握的树你就是牛人了。
今天就聊聊这个”五大经典查找“中的最后一个”二叉排序树“。
1. 概念:
<1> 其实很简单,若根节点有左子树,则左子树的所有节点都比根节点小。
若根节点有右子树,则右子树的所有节点都比根节点大。
<2> 如图就是一个”二叉排序树“,然后对照概念一比较比较。
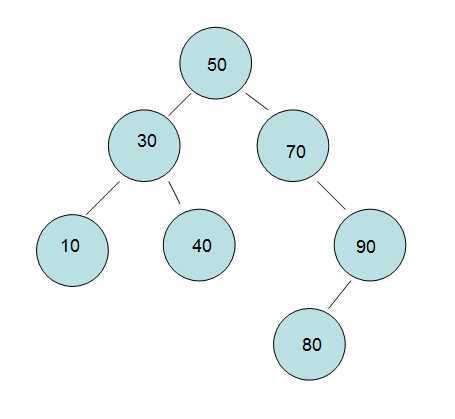
2.实际操作:
我们都知道,对一个东西进行操作,无非就是增删查改,接下来我们就聊聊其中的基本操作。
<1> 插入:相信大家对“排序树”的概念都清楚了吧,那么插入的原理就很简单了。
比如说我们插入一个20到这棵树中。
首先:20跟50比,发现20是老小,不得已,得要归结到50的左子树中去比较。
然后:20跟30比,发现20还是老小。
再然后:20跟10比,发现自己是老大,随即插入到10的右子树中。
最后: 效果呈现图如下:
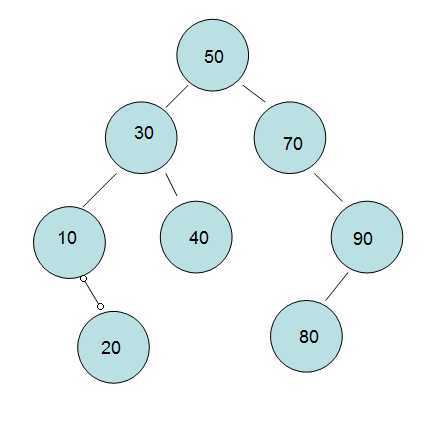
<2>查找:相信懂得了插入,查找就跟容易理解了。
就拿上面一幅图来说,比如我想找到节点10.
首先:10跟50比,发现10是老小,则在50的左子树中找。
然后:10跟30比,发现还是老小,则在30的左子树中找。
再然后: 10跟10比,发现一样,然后就返回找到的信号。
<3>删除:删除节点在树中还是比较麻烦的,主要有三种情况。
《1》 删除的是“叶节点20“,这种情况还是比较简单的,删除20不会破坏树的结构。如图:
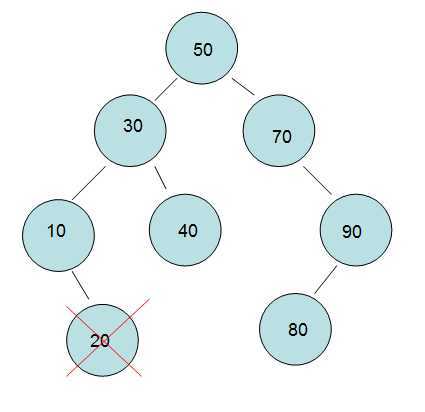
《2》删除”单孩子节点90“,这个情况相比第一种要麻烦一点点,需要把他的孩子顶上去。
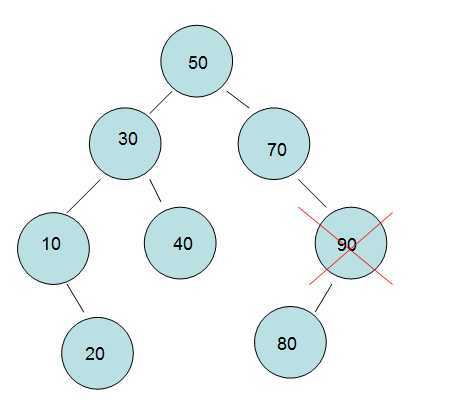
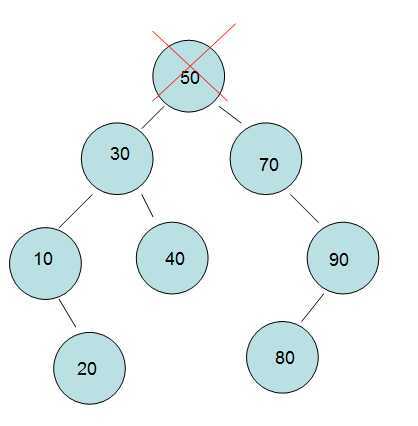
《3》删除“左右孩子都有的节点50”,这个让我在代码编写上纠结了好长时间,问题很直白,
我把50删掉了,谁顶上去了问题,是左孩子呢?还是右孩子呢?还是另有蹊跷?这里我就
坦白吧,不知道大家可否知道“二叉树”的中序遍历,不过这个我会在后面讲的,现在可以当
公式记住吧,就是找到右节点的左子树最左孩子。
比如:首先 找到50的右孩子70。
然后 找到70的最左孩子,发现没有,则返回自己。
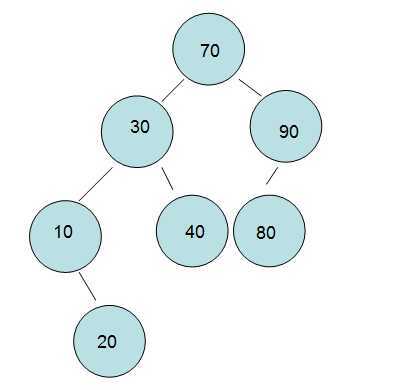
最后 原始图和最终图如下。
3.说了这么多,上代码说话。
1 using System;
2 using System.Collections.Generic;
3 using System.Linq;
4 using System.Text;
5 using System.Diagnostics;
6
7 namespace TreeSearch
8 {
9 class Program
10 {
11 static void Main(string[] args)
12 {
13 List<int> list = new List<int>() { 50, 30, 70, 10, 40, 90, 80 };
14
15 //创建二叉遍历树
16 BSTree bsTree = CreateBST(list);
17
18 Console.Write("中序遍历的原始数据:");
19
20 //中序遍历
21 LDR_BST(bsTree);
22
23 Console.WriteLine("\n---------------------------------------------------------------------------n");
24
25 //查找一个节点
26 Console.WriteLine("\n10在二叉树中是否包含:" + SearchBST(bsTree, 10));
27
28 Console.WriteLine("\n---------------------------------------------------------------------------n");
29
30 bool isExcute = false;
31
32 //插入一个节点
33 InsertBST(bsTree, 20, ref isExcute);
34
35 Console.WriteLine("\n20插入到二叉树,中序遍历后:");
36
37 //中序遍历
38 LDR_BST(bsTree);
39
40 Console.WriteLine("\n---------------------------------------------------------------------------n");
41
42 Console.Write("删除叶子节点 20, \n中序遍历后:");
43
44 //删除一个节点(叶子节点)
45 DeleteBST(ref bsTree, 20);
46
47 //再次中序遍历
48 LDR_BST(bsTree);
49
50 Console.WriteLine("\n****************************************************************************\n");
51
52 Console.WriteLine("删除单孩子节点 90, \n中序遍历后:");
53
54 //删除单孩子节点
55 DeleteBST(ref bsTree, 90);
56
57 //再次中序遍历
58 LDR_BST(bsTree);
59
60 Console.WriteLine("\n****************************************************************************\n");
61
62 Console.WriteLine("删除根节点 50, \n中序遍历后:");
63 //删除根节点
64 DeleteBST(ref bsTree, 50);
65
66 LDR_BST(bsTree);
67
68 }
69
70 ///<summary>
71 /// 定义一个二叉排序树结构
72 ///</summary>
73 public class BSTree
74 {
75 public int data;
76 public BSTree left;
77 public BSTree right;
78 }
79
80 ///<summary>
81 /// 二叉排序树的插入操作
82 ///</summary>
83 ///<param name="bsTree">排序树</param>
84 ///<param name="key">插入数</param>
85 ///<param name="isExcute">是否执行了if语句</param>
86 static void InsertBST(BSTree bsTree, int key, ref bool isExcute)
87 {
88 if (bsTree == null)
89 return;
90
91 //如果父节点大于key,则遍历左子树
92 if (bsTree.data > key)
93 InsertBST(bsTree.left, key, ref isExcute);
94 else
95 InsertBST(bsTree.right, key, ref isExcute);
96
97 if (!isExcute)
98 {
99 //构建当前节点
100 BSTree current = new BSTree()
101 {
102 data = key,
103 left = null,
104 right = null
105 };
106
107 //插入到父节点的当前元素
108 if (bsTree.data > key)
109 bsTree.left = current;
110 else
111 bsTree.right = current;
112
113 isExcute = true;
114 }
115
116 }
117
118 ///<summary>
119 /// 创建二叉排序树
120 ///</summary>
121 ///<param name="list"></param>
122 static BSTree CreateBST(List<int> list)
123 {
124 //构建BST中的根节点
125 BSTree bsTree = new BSTree()
126 {
127 data = list[0],
128 left = null,
129 right = null
130 };
131
132 for (int i = 1; i < list.Count; i++)
133 {
134 bool isExcute = false;
135 InsertBST(bsTree, list[i], ref isExcute);
136 }
137 return bsTree;
138 }
139
140 ///<summary>
141 /// 在排序二叉树中搜索指定节点
142 ///</summary>
143 ///<param name="bsTree"></param>
144 ///<param name="key"></param>
145 ///<returns></returns>
146 static bool SearchBST(BSTree bsTree, int key)
147 {
148 //如果bsTree为空,说明已经遍历到头了
149 if (bsTree == null)
150 return false;
151
152 if (bsTree.data == key)
153 return true;
154
155 if (bsTree.data > key)
156 return SearchBST(bsTree.left, key);
157 else
158 return SearchBST(bsTree.right, key);
159 }
160
161 ///<summary>
162 /// 中序遍历二叉排序树
163 ///</summary>
164 ///<param name="bsTree"></param>
165 ///<returns></returns>
166 static void LDR_BST(BSTree bsTree)
167 {
168 if (bsTree != null)
169 {
170 //遍历左子树
171 LDR_BST(bsTree.left);
172
173 //输入节点数据
174 Console.Write(bsTree.data + "");
175
176 //遍历右子树
177 LDR_BST(bsTree.right);
178 }
179 }
180
181 ///<summary>
182 /// 删除二叉排序树中指定key节点
183 ///</summary>
184 ///<param name="bsTree"></param>
185 ///<param name="key"></param>
186 static void DeleteBST(ref BSTree bsTree, int key)
187 {
188 if (bsTree == null)
189 return;
190
191 if (bsTree.data == key)
192 {
193 //第一种情况:叶子节点
194 if (bsTree.left == null && bsTree.right == null)
195 {
196 bsTree = null;
197 return;
198 }
199 //第二种情况:左子树不为空
200 if (bsTree.left != null && bsTree.right == null)
201 {
202 bsTree = bsTree.left;
203 return;
204 }
205 //第三种情况,右子树不为空
206 if (bsTree.left == null && bsTree.right != null)
207 {
208 bsTree = bsTree.right;
209 return;
210 }
211 //第四种情况,左右子树都不为空
212 if (bsTree.left != null && bsTree.right != null)
213 {
214 var node = bsTree.right;
215
216 //找到右子树中的最左节点
217 while (node.left != null)
218 {
219 //遍历它的左子树
220 node = node.left;
221 }
222
223 //交换左右孩子
224 node.left = bsTree.left;
225
226 //判断是真正的叶子节点还是空左孩子的父节点
227 if (node.right == null)
228 {
229 //删除掉右子树最左节点
230 DeleteBST(ref bsTree, node.data);
231
232 node.right = bsTree.right;
233 }
234 //重新赋值一下
235 bsTree = node;
236
237 }
238 }
239
240 if (bsTree.data > key)
241 {
242 DeleteBST(ref bsTree.left, key);
243 }
244 else
245 {
246 DeleteBST(ref bsTree.right, key);
247 }
248 }
249 }
250 }
运行结果:
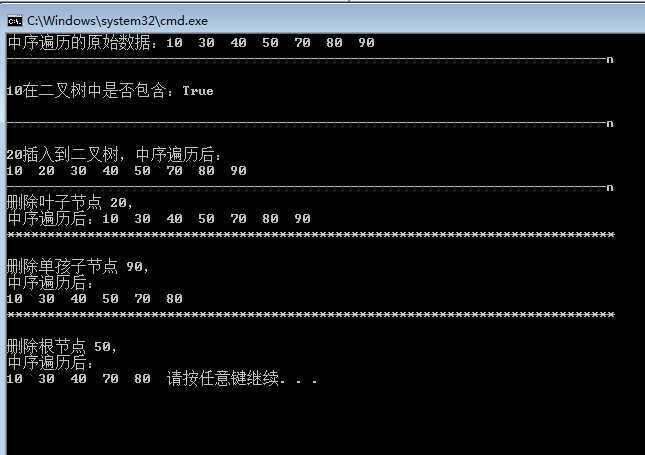
值的注意的是:二叉排序树同样采用“空间换时间”的做法。
突然发现,二叉排序树的中序遍历同样可以排序数组,呵呵,不错!
PS: 插入操作:O(LogN)。
删除操作:O(LogN)。
查找操作:O(LogN)。
标签:
原文地址:http://www.cnblogs.com/lonelyxmas/p/4227676.html