标签:
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 12490 | Accepted: 5265 |
Description
On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.
Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
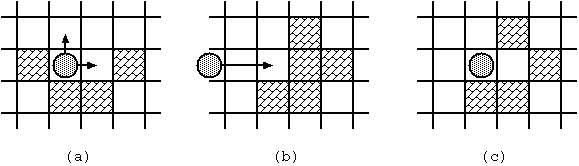
Fig. 2: Stone movements
Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).
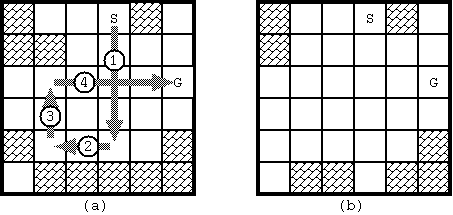
Fig. 3: The solution for Fig. D-1 and the final board configuration
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.
Each dataset is formatted as follows.
the width(=w) and the height(=h) of the board
First row of the board
...
h-th row of the board
The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.
Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.
0 vacant square 1 block 2 start position 3 goal position
The dataset for Fig. D-1 is as follows:
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
Output
For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.
Sample Input
2 1 3 2 6 6 1 0 0 2 1 0 1 1 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 6 1 1 1 2 1 1 3 6 1 1 0 2 1 1 3 12 1 2 0 1 1 1 1 1 1 1 1 1 3 13 1 2 0 1 1 1 1 1 1 1 1 1 1 3 0 0
Sample Output
1 4 -1 4 10 -1
题意:给你一个冰壶游戏的规则,让你输出最少移动多少次冰壶可以赢得游戏。
规则中要注意几点:
1.冰壶砸到墙会停下,然后墙消失。
2.冰壶不需要撞墙以后停在终点,只需到达g点就可以自动停下,赢得游戏。
一个易错点:2点是起点,在dfs过程中要注意2点的特殊性,它不是1(墙),别以外只要遇到非1点总要停下。
因为冰壶砸到墙会停下,然后墙消失。所以图是随时改变的,用dfs的回溯可以很好解决,虽然这题有点像bfs,但是图随时改变,用bfs还要备份图,时间和空间复杂度大大提高。
//168 KB 110 ms
#include<cstdio>
#include<cstring>
#define inf 0x7fffffff
int sx,sy,minn,r,c;
int mapp[25][25];
int dir[4][2]={{-1,0},{1,0},{0,1},{0,-1}};
void ini()
{
minn=inf;
memset(mapp,-1,sizeof(mapp));
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++){
scanf("%d",&mapp[i][j]);
if(mapp[i][j]==2) sx=i,sy=j;
}
}
void dfs(int x,int y,int cnt)
{
cnt++;
if(cnt>10) return ;
for(int i=0;i<4;i++){
int tx=x+dir[i][0];
int ty=y+dir[i][1];
if(mapp[tx][ty]==1) continue; //被墙壁挡住不能向这个方向抛。
while(mapp[tx][ty]==0||mapp[tx][ty]==2){ //易错,因为除了0以外,2这个点也是没墙壁的,易错。
tx+=dir[i][0];
ty+=dir[i][1];
}
if(mapp[tx][ty]<0) continue;
if(mapp[tx][ty]==1){
mapp[tx][ty]=0;
dfs(tx-dir[i][0],ty-dir[i][1],cnt);
mapp[tx][ty]=1;
}
if(mapp[tx][ty]==3){
if(cnt<minn) minn=cnt;
continue;
}
}
}
int main()
{
// freopen("1.in","r",stdin);
while(~scanf("%d%d",&c,&r)&&(c||r)){
ini();
dfs(sx,sy,0);
if(minn<inf) printf("%d\n",minn);
else printf("-1\n");
}
return 0;
}
标签:
原文地址:http://blog.csdn.net/kalilili/article/details/42974455