标签:
凸包算法是计算几何中的最经典问题之一了。给定一个点集,计算其凸包。凸包是什么就不罗嗦了
本文给出了《计算几何——算法与应用》中一书所列凸包算法的Python实现和Matlab实现,并给出了一个Matlab动画演示程序。
啊,实现谁都会实现啦╮(╯▽╰)╭,但是演示就不一定那么好做了。
算法CONVEXHULL(P) 输入:平面点集P 输出:由CH(P)的所有顶点沿顺时针方向组成的一个列表 1. 根据x-坐标,对所有点进行排序,得到序列p1, …, pn 2. 在Lupper中加入p1和p2(p1在前) 3. for(i←3 ton) 4. do 在Lupper中加入pi 5. while(Lupper中至少还有三个点,而且最末尾的三个点所构成的不是一个右拐) 6. do 将倒数第二个顶点从Lupper中删去 7. 在Llower 中加入pn和pn-1(pn在前) 8. for(i←n-2 downto1) 9. do 在Llower 中加入pi 10. while(Llower 中至少还有三个点,而且最末尾的三个点所构成的不是一个右拐) 11. do 将倒数第二个顶点从Llower 中删去 12. 将第一个和最后一个点从Llower 中删去 (以免在上凸包与下凸包联接之后,出现重复顶点) 13. 将Llower 联接到Lupper后面(将由此得到的列表记为L) 14. return(L)
看看,不是很多的样子是吧。
这里面需要说明的地方只有一点,那就是方向的判定问题。
设有三个点P,Q,R,现需求R位于向量PQ的左侧还是右侧(或者R在PQ上)。
计算PR与PQ的叉积,也就是外积。
如果将向量PR以P为旋转中心旋转只向量PQ的方向走过一个正角(逆时针),意味着R在PQ的右侧,此时外积为正。
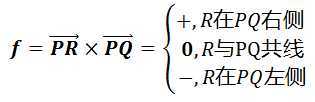
另外需要注意的是,如果在凸包上有三点共线的情况,在本例中三点是均位于凸包边界点集中的。如果想避免这一点,可以通过微量抖动数据的方式解决。
废话不多说,Python实现如下:
1 #!/usr/bin/env python 2 # coding: gbk 3 4 ######################################################################## 5 #Author: Feng Ruohang 6 #Create: 2014/10/02 13:39 7 #Digest: Computate the convex hull of a given point list 8 ######################################################################## 9 10 11 direction = lambda m: (m[2][0] - m[0][0]) * (m[1][1] - m[0][1]) - (m[1][0] - m[0][0]) * (m[2][1] - m[0][1]) 12 ‘‘‘ 13 A Quick Side_check version Using Lambda expression 14 Input: Given a list of three point : m should like [(p_x,p_y), (q_x,q_y), (r_x,r_y)] 15 Output: Return a Number to indicate whether r on the right side of vector(PQ). 16 Positive means r is on the right side of vector(PQ). 17 This is negative of cross product of PQ and PR: Defined by:(Qx-Px)(Ry-Py)-(Rx-Px)(Qy-Py) 18 Which ‘negative‘ indicate PR is clockwise to PQ, equivalent to R is on the right side of PQ 19 ‘‘‘ 20 21 22 def convex_hull(point_list): 23 ‘‘‘ 24 Input: Given a point List: A List of Truple (x,y) 25 Output: Return a point list: A List of Truple (x,y) which is CONVEX HULL of input 26 For the sake of effeciency, There is no error check mechanism here. Please catch outside 27 ‘‘‘ 28 n = len(point_list) #Total Length 29 point_list.sort() 30 31 #Valid Check: 32 if n < 3: 33 return point_list 34 35 #Building Upper Hull: Initialized with first two point 36 upper_hull = point_list[0:1] 37 for i in range(2, n): 38 upper_hull.append(point_list[i]) 39 while len(upper_hull) >= 3 and not direction(upper_hull[-3:]): 40 del upper_hull[-2] 41 42 #Building Lower Hull: Initialized with last two point 43 lower_hull = [point_list[-1], point_list[-2]] 44 for i in range(n - 3, -1, -1): #From the i-3th to the first point 45 lower_hull.append(point_list[i]) 46 while len(lower_hull) >= 3 and not direction(lower_hull[-3:]): 47 del lower_hull[-2] 48 upper_hull.extend(lower_hull[1:-1]) 49 return upper_hull 50 51 52 #========Unit Test: 53 if __name__ == ‘__main__‘: 54 test_data = [(i, i ** 2) for i in range(1, 100)] 55 result = convex_hull(test_data) 56 print result 57 58 2015年1月23日
使用很简单,看DocString就行。
下面顺便给出了Matlab 的实现,以及可视化的算法演示:
效果就是个小动画,像这样吧。
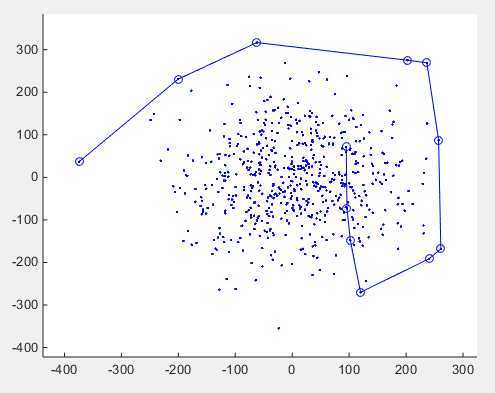
Matlab的凸包算法有三个文件:
side_check2:检查三个点构成的弯折的方向
Convex_hull: 凸包算法Matlab实现
Convex_hull_demo:凸包算法的演示。
拷在一个目录里
运行convex_hull_demo( randn(200,2)*100); 就可以看到可视化演示了
这个是辅助函数
%filename: side_check2.m
%Input: Matrix of three point: (2x3 or 3x2)
% P(p_x,p_y),Q(q_x,q_y),R(r_x,r_y)
%Output: 如果P Q R三点构成一个右拐,返回True
% 右拐意味着点R在PQ向量的右侧.此时
function result = side_check2(D)
if all(size(D) ~= [3,2])
if all(size(D)==[2,3])
D = D‘;
else
error(‘error dimension‘)
end
end
result = (det([[1;1;1], D]) < 0 );
这个是纯算法实现。
%filename: convex_hull.m
%CONVEX_HULL
%INPUT: Point Set:(n x 2)
%OUPUT: HULL Point List: (x x 2)
function L=t(P)
[num,dimension] = size(P);
if dimension ~= 2
error(‘dimension error‘)
end
P = sortrows(P,[1,2]);
%if there is only one or two point remain,return it
if num < 3
L = P;
return
end
%STEP ONE: Upper Hull:
L_upper = P([1,2],:); %Take first two points
for i = 3:num
L_upper = [L_upper;P(i,:)]; %add the point into list
while size(L_upper,1) >= 3
l_size = size(L_upper,1);
if det([ones(3,1),L_upper(l_size-2:l_size,:)])= 3
l_size = size(L_lower,1);
if det([ones(3,1),L_lower(l_size-2:l_size,:)])
这个是演示:
%CONVEX_HULL
%INPUT: Point Set:(n x 2)
%OUPUT: HULL Point List: (x x 2)
%Samples: convex_hull_demo( randn(200,2)*100)
function L=convex_hull_demo(P)
%Test Data
%data_size = data_size
%P = randi([-50,50],[data_size,2]);
[num,dimension] = size(P);
if dimension ~= 2
error(‘dimension error‘)
end
P = sortrows(P,[1,2]);
%====Visual Lization
board_left = min(P(:,1));
board_right = max(P(:,1));
board_bottom = min(P(:,2));
board_up = max(P(:,2));
x_padding = (board_right- board_left)*0.1;
y_padding = (board_up- board_bottom)*0.1;
plot_range= [board_left - x_padding,board_right + x_padding,board_bottom-y_padding,board_up+y_padding];
clf;
scatter(P(:,1),P(:,2),‘b.‘);
axis(plot_range);
hold on
%====VisualLization
%if there is only one or two point remain,return it
if num < 3
L = P;
end
%STEP ONE: Upper Hull:
L_upper = P([1,2],:); %Take first two points
hull_handle = plot(L_upper(:,1),L_upper(:,2),‘ob-‘);
for i = 3:num
L_upper = [L_upper;P(i,:)]; %add the point into list
while size(L_upper,1) >= 3
l_size = size(L_upper,1);
if side_check2(L_upper(l_size-2:l_size,:)) %Check if it is valid
break; %Quit if Valid
else
L_upper(l_size-1,:) = []; %Remove the inner point and continue if not
end
set(hull_handle,‘XData‘,L_upper(:,1),‘YData‘,L_upper(:,2));drawnow;
end
set(hull_handle,‘XData‘,L_upper(:,1),‘YData‘,L_upper(:,2));drawnow;
end
%Visualization
plot(L_upper(:,1),L_upper(:,2),‘bo-‘);
%Visualization
%STEP Two: Build the lower hull
L_lower = [P([num,num-1],:)]; % Add P(n) and P(n-1)
set(hull_handle,‘XData‘,L_lower(:,1),‘YData‘,L_lower(:,2));drawnow;
for i = num-2:-1:1
L_lower = [L_lower;P(i,:)];
while size(L_lower,1) >= 3
l_size = size(L_lower,1);
if side_check2(L_lower(l_size-2:l_size,:)) %Check if it is valid
break; %Quit if Valid
else
L_lower(l_size-1,:) = []; %Remove the inner point and continue if not
end
set(hull_handle,‘XData‘,L_lower(:,1),‘YData‘,L_lower(:,2));drawnow;
end
set(hull_handle,‘XData‘,L_lower(:,1),‘YData‘,L_lower(:,2));drawnow;
end
L_lower([1,size(L_lower,1)],:) = [];
if isempty(L_lower)
L = L_upper;
else
L = [L_upper;L_lower(2:size(L_lower,1)-1,:)];
end
hold off;
return
标签:
原文地址:http://www.cnblogs.com/Vonng/p/4245092.html