算法分析

标签：

想花上一个月的时间将 《算法导论》 这门基础课程学好。主要还是借助于网易公开课上MIT的这门课程，另外还有两本参考书籍，一个讲数据结构，一个讲算法的。这个系列就算作学习笔记加上自己的整理了。

为什么先学习算法分析

几乎所有的算法书籍开篇都会介绍算法分析的知识。它为什么显得如此重要呢？设想，当我们面对别人的算法时，不知道怎样去分析它的优点及缺点，那我至少相信我们很难对此算法做出相应的优化。算法分析是学习算法的基础，它将会贯穿整个学习的过程，所以，必须先要过这一关。（其实，也就是一点点数学知识 ^_^!）下面还是先举个例子来看看不同算法之间的差异吧！相信会震撼到你！

问题描述：

输入一组整数，求出这组数字子序列和中最大值。也就是只要求出最大子序列的和，不必求出最大的那个序列。例如：

序列：-2 11 -4 13 -5 -2，则最大子序列和为20。

序列：-6 2 4 -7 5 3 2 -1 6 -9 10 -2，则最大子序列和为16。

关于这个问题的解法非常多，下面就是我用四种不同的方法的python代码。（为什么选python, 主要是由于它简单清晰，接近自然语言）。

#穷举法1
def function1(data):
      N = len(data)
      maxsum = data[0]
      for i in xrange(0, N):
            for j in xrange(0, i + 1):
                  tmp = 0
                  for k in xrange(j, i + 1):
                        tmp += data[k]
                        maxsum = max(maxsum, tmp)
      return maxsum


#穷举法2
def function2(data):
      N = len(data)
      maxsum = data[0]
      for i in xrange(0, N):
            tmp = 0
            for j in xrange(i, N):
                  tmp += data[j]
                  maxsum = max(tmp, maxsum)
      return maxsum


#分治法
def function3(data, left, right):
      if left == right:
            return data[left]

      center = int((left + right) / 2)
      max_left = function3(data, left, center)
      max_right = function3(data, center + 1, right)
      
      max_tmp_left = data[center]
      tmp_left = 0
      max_tmp_right = data[center + 1]
      tmp_right = 0
      for i in xrange(center, left - 1, -1):
            tmp_left += data[i]
            if(tmp_left >= max_tmp_left):
                  max_tmp_left = tmp_left
      for i in xrange(center + 1, right + 1):
            tmp_right += data[i]
            if(tmp_right >= max_tmp_right):
                  max_tmp_right = tmp_right

      return max(max_left, max_right, max_tmp_left + max_tmp_right)


#动态规划
def function4(data):
      maxsum = data[0]
      tmp = 0
      n = len(data)
      for i in xrange(n):
            tmp += data[i]
            maxsum = max(maxsum, tmp)
            if tmp < 0:
                  tmp = 0
      return maxsum

View Code

它们的运行比较时间见下面的表格（单位：ms）：

方法\输入大小　　10　　　　　　100　　　　　　1000
　　1　　　　　　0.18　　　　　98　　　　 　　90391
　　2　　　　　　0.04　　　　　3　　　　　　　270
　　3　　　　　　0.036　　　　0.56　　　　　 6.23
　　4　　　　　　0.006　　　　0.05　　　　　 0.55　　

没错，就是这么神奇，最快的方法与最慢的算法竟然相差那么多，好的方法能让事情变得更高效，带来更好的体验。这便是算法的威力。

想要更加清楚的认识不同的算法，首先还是必须对它进行一定的分析。作为分析而言，比较它们具体的运行时间能说明一定的问题，但是这还不够，且不说运行时间与机器的速度，指令的处理时间等等因素有关，这种做法并不能在数学的层面，在更为抽象的层面给出它们的本质。这里都会借助于数学中的一套理论（其实，很简单）来帮助我们分析认识算法。下面会进行简单的介绍。

三个数学概念

下面的描述并非用真正严格意义上的数学语言来描述，更多的是一种概念上的理解与近似，难免会有不准确的地方。

• $$f(n) = O(g(n))$$: 存在c > 0, 当n > n0时，$$0\leq f(n)\leq cg(n)$$。可以简单的认为，f(n)最多最多是与g(n)在同一个数量级上。
• $$\Omega(f(n))= g(n)$$: 存在c > 0, n0 > 0, 使得$$0\leq cg(n) \leq f(n)$$。可以简答的认为，f(n)至少至少是与g(n)在同一个数量级上的。
• $$f(n) = \Theta(g(n))$$: 这是上面两种情况的综合，表示f(n)与g(n)在同一个数量级上，可以相差 一个常数或者常数项。

这几个符号会在后面的课程中用的非常之多，理解起来也不困难，并且对只进行算法分析的我们也已经够用了。

解递归的方法

递归在算法中属于一个重要的内容，可以说是无处不在。同时它的分析也显得不是那么轻松，在这里首先介绍一个形象一点的解法叫做 “递归树”，其次再介绍一个更为通用的方法叫做 “主方法”，类似于数学公式，以后遇到递归问题就可以直接套用公式就可以了。

1 递归树解法

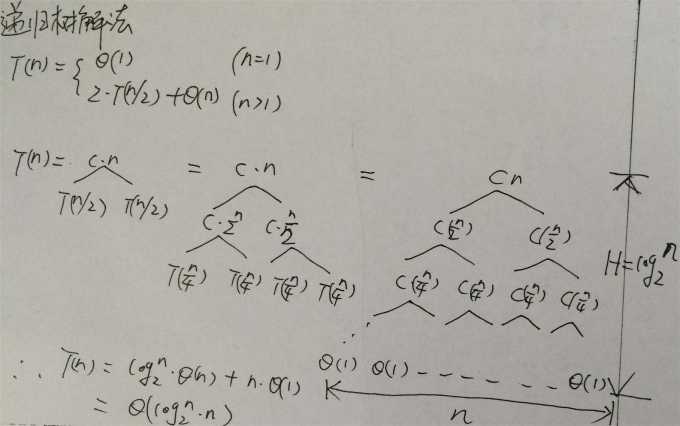
2 主方法

主方法对形如 T(n)=aT(n/b)+f(n)这样的递归式子进行了总结，它可以使用递归树推导得出，这样就直接给出结论

• case1: $$f(n) = O({n}^{log{b}^{(a - \varepsilon )}})$$,  这个时候f(n)阶数比较低，不会占主导地位，所以$$T(n)=\Theta (log{b}^{a})$$
• case2: $$f(n) = \Theta({n}^{log{b}^{a}})$$, 即他们同阶，这个时候$$T(n) = \Theta ({n}^{log{b}^{a}})$$
• case3: $$f(n) = \Omega ({n}^{log{b}^{a + \varepsilon }})$$, 这个时候f(n)占主导地位，所以$$T(n) = \Theta (f(n))$$

总结

算法分析的相关知识到这里就介绍完了。本来是应该再多举几个例子来巩固下这部分知识的，但是考虑到后续的课程中几乎都离不开算法分析，所以想将更多的实践放到后面，希望能够很好的运用这部分知识。

算法分析

标签：

原文地址：http://www.cnblogs.com/Gru--/p/4268878.html