更多数据挖掘代码:https://github.com/linyiqun/DataMiningAlgorithm
BIRCH算法本身上属于一种聚类算法,不过他克服了一些K-Means算法的缺点,比如说这个k的确定,因为这个算法事先本身就没有设定有多少个聚类。他是通过CF-Tree,(ClusterFeature-Tree)聚类特征树实现的。BIRCH的一个重要考虑是最小化I/O,通过扫描数据库,建立一棵存放于内存的初始CF-树,可以看做多数据的多层压缩。
说到算法原理,首先就要先知道,什么是聚类特征,何为聚类特征,定义如下:
CF = <n, LS, SS>
聚类特征为一个3维向量,n为数据点总数,LS为n个点的线性和,SS为n个点的平方和。因此又可以得到
x0 = LS/n为簇的中心,以此计算簇与簇之间的距离。
簇内对象的平均距离簇直径,这个可以用阈值T限制,保证簇的一个整体的紧凑程度。簇和簇之间可以进行叠加,其实就是向量的叠加。
在介绍CF-Tree树,要先介绍3个变量,内部节点平衡因子B,叶节点平衡因子L,簇直径阈值T。B是用来限制非叶子节点的子节点数,L是用来限制叶子节点的子簇个数,T是用来限制簇的紧密程度的,比较的是D--簇内平均对象的距离。下面是主要的构造过程:
1、首先读入第一条数据,构造一个叶子节点和一个子簇,子簇包含在叶子节点中。
2、当读入后面的第2条,第3条,封装为一个簇,加入到一个叶子节点时,如果此时的待加入的簇C的簇直径已经大于T,则需要新建簇作为C的兄弟节点,如果作为兄弟节点,如果此时的叶子节点的孩子节点超过阈值L,则需对叶子节点进行分裂。分裂的规则是选出簇间距离最大的2个孩子,分别作为2个叶子,然后其他的孩子按照就近分配。非叶子节点的分裂规则同上。具体可以对照后面我写的代码。
3、最终的构造模样大致如此:
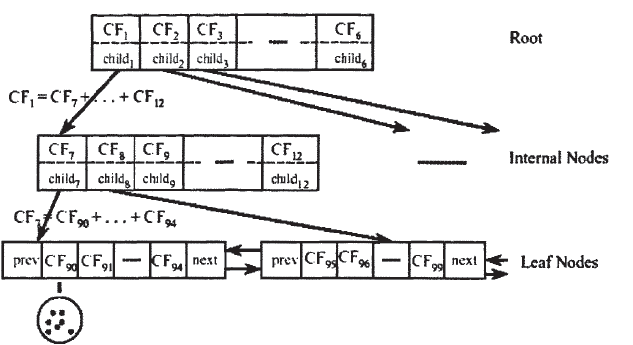
1、算法只需扫描一遍就可以得到一个好的聚类效果,而且不需事先设定聚类个数。
2、聚类通过聚类特征树的形式,一定程度上保存了对数据的压缩。
1、该算法比较适合球形的簇,如果簇不是球形的,则聚簇的效果将不会很好。
算法的代码实现:
下面提供部分核心代码(如果想获取所有的代码,请点击我的数据挖掘代码):
数据的输入:
5.1 3.5 1.4 0.2 4.9 3.0 1.4 0.2 4.7 3.2 1.3 0.8 4.6 3.1 1.5 0.8 5.0 3.6 1.8 0.6 4.7 3.2 1.4 0.8
ClusteringFeature.java:
package DataMining_BIRCH;
import java.util.ArrayList;
/**
* 聚类特征基本属性
*
* @author lyq
*
*/
public abstract class ClusteringFeature {
// 子类中节点的总数目
protected int N;
// 子类中N个节点的线性和
protected double[] LS;
// 子类中N个节点的平方和
protected double[] SS;
//节点深度,用于CF树的输出
protected int level;
public int getN() {
return N;
}
public void setN(int n) {
N = n;
}
public double[] getLS() {
return LS;
}
public void setLS(double[] lS) {
LS = lS;
}
public double[] getSS() {
return SS;
}
public void setSS(double[] sS) {
SS = sS;
}
protected void setN(ArrayList<double[]> dataRecords) {
this.N = dataRecords.size();
}
public int getLevel() {
return level;
}
public void setLevel(int level) {
this.level = level;
}
/**
* 根据节点数据计算线性和
*
* @param dataRecords
* 节点数据记录
*/
protected void setLS(ArrayList<double[]> dataRecords) {
int num = dataRecords.get(0).length;
double[] record;
LS = new double[num];
for (int j = 0; j < num; j++) {
LS[j] = 0;
}
for (int i = 0; i < dataRecords.size(); i++) {
record = dataRecords.get(i);
for (int j = 0; j < record.length; j++) {
LS[j] += record[j];
}
}
}
/**
* 根据节点数据计算平方
*
* @param dataRecords
* 节点数据
*/
protected void setSS(ArrayList<double[]> dataRecords) {
int num = dataRecords.get(0).length;
double[] record;
SS = new double[num];
for (int j = 0; j < num; j++) {
SS[j] = 0;
}
for (int i = 0; i < dataRecords.size(); i++) {
record = dataRecords.get(i);
for (int j = 0; j < record.length; j++) {
SS[j] += record[j] * record[j];
}
}
}
/**
* CF向量特征的叠加,无须考虑划分
*
* @param node
*/
protected void directAddCluster(ClusteringFeature node) {
int N = node.getN();
double[] otherLS = node.getLS();
double[] otherSS = node.getSS();
if(LS == null){
this.N = 0;
LS = new double[otherLS.length];
SS = new double[otherLS.length];
for(int i=0; i<LS.length; i++){
LS[i] = 0;
SS[i] = 0;
}
}
// 3个数量上进行叠加
for (int i = 0; i < LS.length; i++) {
LS[i] += otherLS[i];
SS[i] += otherSS[i];
}
this.N += N;
}
/**
* 计算簇与簇之间的距离即簇中心之间的距离
*
* @return
*/
protected double computerClusterDistance(ClusteringFeature cluster) {
double distance = 0;
double[] otherLS = cluster.LS;
int num = N;
int otherNum = cluster.N;
for (int i = 0; i < LS.length; i++) {
distance += (LS[i] / num - otherLS[i] / otherNum)
* (LS[i] / num - otherLS[i] / otherNum);
}
distance = Math.sqrt(distance);
return distance;
}
/**
* 计算簇内对象的平均距离
*
* @param records
* 簇内的数据记录
* @return
*/
protected double computerInClusterDistance(ArrayList<double[]> records) {
double sumDistance = 0;
double[] data1;
double[] data2;
// 数据总数
int totalNum = records.size();
for (int i = 0; i < totalNum - 1; i++) {
data1 = records.get(i);
for (int j = i + 1; j < totalNum; j++) {
data2 = records.get(j);
sumDistance += computeOuDistance(data1, data2);
}
}
// 返回的值除以总对数,总对数应减半,会重复算一次
return Math.sqrt(sumDistance / (totalNum * (totalNum - 1) / 2));
}
/**
* 对给定的2个向量,计算欧式距离
*
* @param record1
* 向量点1
* @param record2
* 向量点2
*/
private double computeOuDistance(double[] record1, double[] record2) {
double distance = 0;
for (int i = 0; i < record1.length; i++) {
distance += (record1[i] - record2[i]) * (record1[i] - record2[i]);
}
return distance;
}
/**
* 聚类添加节点包括,超出阈值进行分裂的操作
*
* @param clusteringFeature
* 待添加聚簇
*/
public abstract void addingCluster(ClusteringFeature clusteringFeature);
}
BIRCHTool.java:
package DataMining_BIRCH;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.text.MessageFormat;
import java.util.ArrayList;
import java.util.LinkedList;
/**
* BIRCH聚类算法工具类
*
* @author lyq
*
*/
public class BIRCHTool {
// 节点类型名称
public static final String NON_LEAFNODE = "【NonLeafNode】";
public static final String LEAFNODE = "【LeafNode】";
public static final String CLUSTER = "【Cluster】";
// 测试数据文件地址
private String filePath;
// 内部节点平衡因子B
public static int B;
// 叶子节点平衡因子L
public static int L;
// 簇直径阈值T
public static double T;
// 总的测试数据记录
private ArrayList<String[]> totalDataRecords;
public BIRCHTool(String filePath, int B, int L, double T) {
this.filePath = filePath;
this.B = B;
this.L = L;
this.T = T;
readDataFile();
}
/**
* 从文件中读取数据
*/
private void readDataFile() {
File file = new File(filePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
totalDataRecords = new ArrayList<>();
for (String[] array : dataArray) {
totalDataRecords.add(array);
}
}
/**
* 构建CF聚类特征树
*
* @return
*/
private ClusteringFeature buildCFTree() {
NonLeafNode rootNode = null;
LeafNode leafNode = null;
Cluster cluster = null;
for (String[] record : totalDataRecords) {
cluster = new Cluster(record);
if (rootNode == null) {
// CF树只有1个节点的时候的情况
if (leafNode == null) {
leafNode = new LeafNode();
}
leafNode.addingCluster(cluster);
if (leafNode.getParentNode() != null) {
rootNode = leafNode.getParentNode();
}
} else {
if (rootNode.getParentNode() != null) {
rootNode = rootNode.getParentNode();
}
// 从根节点开始,从上往下寻找到最近的添加目标叶子节点
LeafNode temp = rootNode.findedClosestNode(cluster);
temp.addingCluster(cluster);
}
}
// 从下往上找出最上面的节点
LeafNode node = cluster.getParentNode();
NonLeafNode upNode = node.getParentNode();
if (upNode == null) {
return node;
} else {
while (upNode.getParentNode() != null) {
upNode = upNode.getParentNode();
}
return upNode;
}
}
/**
* 开始构建CF聚类特征树
*/
public void startBuilding() {
// 树深度
int level = 1;
ClusteringFeature rootNode = buildCFTree();
setTreeLevel(rootNode, level);
showCFTree(rootNode);
}
/**
* 设置节点深度
*
* @param clusteringFeature
* 当前节点
* @param level
* 当前深度值
*/
private void setTreeLevel(ClusteringFeature clusteringFeature, int level) {
LeafNode leafNode = null;
NonLeafNode nonLeafNode = null;
if (clusteringFeature instanceof LeafNode) {
leafNode = (LeafNode) clusteringFeature;
} else if (clusteringFeature instanceof NonLeafNode) {
nonLeafNode = (NonLeafNode) clusteringFeature;
}
if (nonLeafNode != null) {
nonLeafNode.setLevel(level);
level++;
// 设置子节点
if (nonLeafNode.getNonLeafChilds() != null) {
for (NonLeafNode n1 : nonLeafNode.getNonLeafChilds()) {
setTreeLevel(n1, level);
}
} else {
for (LeafNode n2 : nonLeafNode.getLeafChilds()) {
setTreeLevel(n2, level);
}
}
} else {
leafNode.setLevel(level);
level++;
// 设置子聚簇
for (Cluster c : leafNode.getClusterChilds()) {
c.setLevel(level);
}
}
}
/**
* 显示CF聚类特征树
*
* @param rootNode
* CF树根节点
*/
private void showCFTree(ClusteringFeature rootNode) {
// 空格数,用于输出
int blankNum = 5;
// 当前树深度
int currentLevel = 1;
LinkedList<ClusteringFeature> nodeQueue = new LinkedList<>();
ClusteringFeature cf;
LeafNode leafNode;
NonLeafNode nonLeafNode;
ArrayList<Cluster> clusterList = new ArrayList<>();
String typeName;
nodeQueue.add(rootNode);
while (nodeQueue.size() > 0) {
cf = nodeQueue.poll();
if (cf instanceof LeafNode) {
leafNode = (LeafNode) cf;
typeName = LEAFNODE;
if (leafNode.getClusterChilds() != null) {
for (Cluster c : leafNode.getClusterChilds()) {
nodeQueue.add(c);
}
}
} else if (cf instanceof NonLeafNode) {
nonLeafNode = (NonLeafNode) cf;
typeName = NON_LEAFNODE;
if (nonLeafNode.getNonLeafChilds() != null) {
for (NonLeafNode n1 : nonLeafNode.getNonLeafChilds()) {
nodeQueue.add(n1);
}
} else {
for (LeafNode n2 : nonLeafNode.getLeafChilds()) {
nodeQueue.add(n2);
}
}
} else {
clusterList.add((Cluster)cf);
typeName = CLUSTER;
}
if (currentLevel != cf.getLevel()) {
currentLevel = cf.getLevel();
System.out.println();
System.out.println("|");
System.out.println("|");
}else if(currentLevel == cf.getLevel() && currentLevel != 1){
for (int i = 0; i < blankNum; i++) {
System.out.print("-");
}
}
System.out.print(typeName);
System.out.print("N:" + cf.getN() + ", LS:");
System.out.print("[");
for (double d : cf.getLS()) {
System.out.print(MessageFormat.format("{0}, ", d));
}
System.out.print("]");
}
System.out.println();
System.out.println("*******最终分好的聚簇****");
//显示已经分好类的聚簇点
for(int i=0; i<clusterList.size(); i++){
System.out.println("Cluster" + (i+1) + ":");
for(double[] point: clusterList.get(i).getData()){
System.out.print("[");
for (double d : point) {
System.out.print(MessageFormat.format("{0}, ", d));
}
System.out.println("]");
}
}
}
}
由于代码量比较大,剩下的LeafNode.java,NonLeafNode.java, 和Cluster聚簇类可以在我的数据挖掘代码中查看。
结果输出:
【NonLeafNode】N:6, LS:[29, 19.6, 8.8, 3.4, ] | | 【LeafNode】N:3, LS:[14, 9.5, 4.2, 2.4, ]-----【LeafNode】N:3, LS:[15, 10.1, 4.6, 1, ] | | 【Cluster】N:3, LS:[14, 9.5, 4.2, 2.4, ]-----【Cluster】N:1, LS:[5, 3.6, 1.8, 0.6, ]-----【Cluster】N:2, LS:[10, 6.5, 2.8, 0.4, ] *******最终分好的聚簇**** Cluster1: [4.7, 3.2, 1.3, 0.8, ] [4.6, 3.1, 1.5, 0.8, ] [4.7, 3.2, 1.4, 0.8, ] Cluster2: [5, 3.6, 1.8, 0.6, ] Cluster3: [5.1, 3.5, 1.4, 0.2, ] [4.9, 3, 1.4, 0.2, ]
1、算簇间距离的时候,代了一下公式,发现不对劲,向量的运算不应该是这样的,于是就把他归与簇心之间的距离计算。还有簇内对象的平均距离也没有代入公式,网上的各种版本的向量计算,不知道哪种是对的,又按最原始的方式计算,一对对计算距离,求平均值。
2、算法在节点分裂的时候,如果父节点不为空,需要把自己从父亲中的孩子列表中移除,然后再添加分裂后的2个节点,这里的把自己移除掉容易忘记。
3、节点CF聚类特征值的更新,需要在每次节点的变化时,其所涉及的父类,父类的父类都需要更新,为此用了责任链模式,一个一个往上传,分裂的规则时也用了此模式,需要关注一下。
4、代码将CF聚类特征量进行抽象提取,定义了共有的方法,不过在实现时还是由于节点类型的不同,在实际的过程中需要转化。
5、最后的难点在与测试的复杂,因为程序经过千辛万苦的编写终于完成,但是如何测试时一个大问题,因为要把分裂的情况都测准,需要准确的把握T.,B.L,的设计,尤其是T簇直径,所以在捏造测试的时候自己也是经过很多的手动计算。
在实现的整个完成的过程中 ,我对BIRCH算法的最大的感触就是通过聚类特征,一个新节点从根节点开始,从上往先寻找,离哪个簇近,就被分到哪个簇中,自发的形成了一个比较好的聚簇,这个过程是算法的神奇所在。
原文地址:http://blog.csdn.net/androidlushangderen/article/details/43532111