标签:
K-Means 概念定义:
K-Means 是一种基于距离的排他的聚类划分方法。
上面的 K-Means 描述中包含了几个概念:
K-Means 问题描述:
给定一个 n 个对象的数据集,它可以构建数据的 k 个划分,每个划分就是一个簇,并且 k ≤ n。同时还需满足:
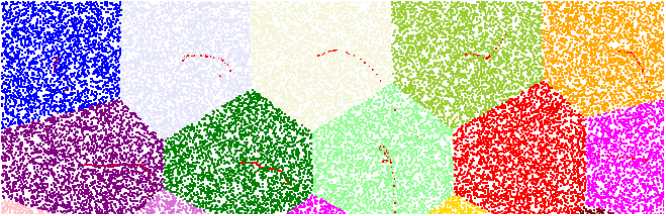
Simply speaking, K-Means clustering is an algorithm to classify or to group your objects based on attributes/features, into K number of groups. K is a positive integer number. The grouping is done by minimizing the sum of squares of distances between data and the corresponding cluster centroid. Thus, the purpose of K-means clustering is to classify the data.
K-Means 算法实现:
K-Means 算法最常见的实现方式是使用迭代式精化启发法的 Lloyd‘s algorithm。
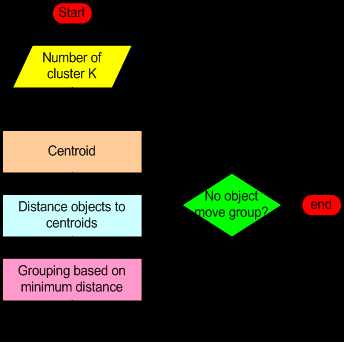
K-Means 优缺点:
当结果簇是密集的,而且簇和簇之间的区别比较明显时,K-Means 的效果较好。对于大数据集,K-Means 是相对可伸缩的和高效的,它的复杂度是 O(nkt),n 是对象的个数,k 是簇的数目,t 是迭代的次数,通常 k << n,且 t << n,所以算法经常以局部最优结束。
K-Means 的最大问题是要求先给出 k 的个数。k 的选择一般基于经验值和多次实验结果,对于不同的数据集,k 的取值没有可借鉴性。另外,K-Means 对孤立点数据是敏感的,少量噪声数据就能对平均值造成极大的影响。
Lloyd‘s algorithm 伪码实现:
1 var m = initialCentroids(x, K); 2 var N = x.length; 3 4 while (!stoppingCriteria) 5 { 6 var w = [][]; 7 8 // calculate membership in clusters 9 for (var n = 1; n <= N; n++) 10 { 11 v = arg min (v0) dist(m[v0], x[n]); 12 w[v].push(n); 13 } 14 15 // recompute the centroids 16 for (var k = 1; k <= K; k++) 17 { 18 m[k] = avg(x in w[k]); 19 } 20 } 21 22 return m;
Lloyd‘s algorithm C# 代码实现:
Code below referenced from Machine Learning Using C# Succinctly by James McCaffrey, and article K-Means Data Clustering Using C#.
1 using System; 2 3 // K-means clustering demo. (‘Lloyd‘s algorithm‘) 4 // Coded using static methods. Normal error-checking removed for clarity. 5 // This code can be used in at least two ways. 6 // You can do a copy-paste and then insert the code into some system. 7 // Or you can wrap the code up in a Class Library. 8 // The single public method is Cluster(). 9 10 namespace ClusteringKMeans 11 { 12 class Program 13 { 14 static void Main(string[] args) 15 { 16 Console.WriteLine("\nBegin k-means clustering demo\n"); 17 18 // real data likely to come from a text file or SQL 19 double[][] raw = new double[20][]; 20 raw[0] = new double[] { 65.0, 220.0 }; 21 raw[1] = new double[] { 73.0, 160.0 }; 22 raw[2] = new double[] { 59.0, 110.0 }; 23 raw[3] = new double[] { 61.0, 120.0 }; 24 raw[4] = new double[] { 75.0, 150.0 }; 25 raw[5] = new double[] { 67.0, 240.0 }; 26 raw[6] = new double[] { 68.0, 230.0 }; 27 raw[7] = new double[] { 70.0, 220.0 }; 28 raw[8] = new double[] { 62.0, 130.0 }; 29 raw[9] = new double[] { 66.0, 210.0 }; 30 raw[10] = new double[] { 77.0, 190.0 }; 31 raw[11] = new double[] { 75.0, 180.0 }; 32 raw[12] = new double[] { 74.0, 170.0 }; 33 raw[13] = new double[] { 70.0, 210.0 }; 34 raw[14] = new double[] { 61.0, 110.0 }; 35 raw[15] = new double[] { 58.0, 100.0 }; 36 raw[16] = new double[] { 66.0, 230.0 }; 37 raw[17] = new double[] { 59.0, 120.0 }; 38 raw[18] = new double[] { 68.0, 210.0 }; 39 raw[19] = new double[] { 61.0, 130.0 }; 40 41 Console.WriteLine("Raw un-clustered data:\n"); 42 Console.WriteLine(" Height Weight"); 43 Console.WriteLine("-------------------"); 44 ShowData(raw, 1, true, true); 45 46 int k = 3; 47 Console.WriteLine("\nSetting k to " + k); 48 49 int[] clustering = Cluster(raw, k); // this is it 50 51 Console.WriteLine("\nK-means clustering complete\n"); 52 53 Console.WriteLine("Final clustering in internal form:\n"); 54 ShowVector(clustering, true); 55 56 Console.WriteLine("Raw data by cluster:\n"); 57 ShowClustered(raw, clustering, k, 1); 58 59 Console.WriteLine("\nEnd k-means clustering demo\n"); 60 Console.ReadLine(); 61 } 62 63 public static int[] Cluster(double[][] rawData, int k) 64 { 65 // k-means clustering 66 // index of return is tuple ID, cell is cluster ID 67 // ex: [2 1 0 0 2 2] means tuple 0 is cluster 2, 68 // tuple 1 is cluster 1, tuple 2 is cluster 0, tuple 3 is cluster 0, etc. 69 // an alternative clustering DS to save space is to use the .NET BitArray class 70 double[][] data = Normalized(rawData); // so large values don‘t dominate 71 72 bool changed = true; // was there a change in at least one cluster assignment? 73 bool success = true; // were all means able to be computed? (no zero-count clusters) 74 75 // init clustering[] to get things started 76 // an alternative is to initialize means to randomly selected tuples 77 // then the processing loop is 78 // loop 79 // update clustering 80 // update means 81 // end loop 82 int[] clustering = InitClustering(data.Length, k, 0); // semi-random initialization 83 double[][] means = Allocate(k, data[0].Length); // small convenience 84 85 int maxCount = data.Length * 10; // sanity check 86 int ct = 0; 87 while (changed == true && success == true && ct < maxCount) 88 { 89 ++ct; // k-means typically converges very quickly 90 success = UpdateMeans(data, clustering, means); // compute new cluster means if possible. no effect if fail 91 changed = UpdateClustering(data, clustering, means); // (re)assign tuples to clusters. no effect if fail 92 } 93 // consider adding means[][] as an out parameter - the final means could be computed 94 // the final means are useful in some scenarios (e.g., discretization and RBF centroids) 95 // and even though you can compute final means from final clustering, in some cases it 96 // makes sense to return the means (at the expense of some method signature uglinesss) 97 // 98 // another alternative is to return, as an out parameter, some measure of cluster goodness 99 // such as the average distance between cluster means, or the average distance between tuples in 100 // a cluster, or a weighted combination of both 101 return clustering; 102 } 103 104 private static double[][] Normalized(double[][] rawData) 105 { 106 // normalize raw data by computing (x - mean) / stddev 107 // primary alternative is min-max: 108 // v‘ = (v - min) / (max - min) 109 110 // make a copy of input data 111 double[][] result = new double[rawData.Length][]; 112 for (int i = 0; i < rawData.Length; ++i) 113 { 114 result[i] = new double[rawData[i].Length]; 115 Array.Copy(rawData[i], result[i], rawData[i].Length); 116 } 117 118 for (int j = 0; j < result[0].Length; ++j) // each col 119 { 120 double colSum = 0.0; 121 for (int i = 0; i < result.Length; ++i) 122 colSum += result[i][j]; 123 double mean = colSum / result.Length; 124 double sum = 0.0; 125 for (int i = 0; i < result.Length; ++i) 126 sum += (result[i][j] - mean) * (result[i][j] - mean); 127 double sd = sum / result.Length; 128 for (int i = 0; i < result.Length; ++i) 129 result[i][j] = (result[i][j] - mean) / sd; 130 } 131 return result; 132 } 133 134 private static int[] InitClustering(int numTuples, int k, int randomSeed) 135 { 136 // init clustering semi-randomly (at least one tuple in each cluster) 137 // consider alternatives, especially k-means++ initialization, 138 // or instead of randomly assigning each tuple to a cluster, pick 139 // numClusters of the tuples as initial centroids/means then use 140 // those means to assign each tuple to an initial cluster. 141 Random random = new Random(randomSeed); 142 int[] clustering = new int[numTuples]; 143 for (int i = 0; i < k; ++i) // make sure each cluster has at least one tuple 144 clustering[i] = i; 145 for (int i = k; i < clustering.Length; ++i) 146 clustering[i] = random.Next(0, k); // other assignments random 147 return clustering; 148 } 149 150 private static double[][] Allocate(int k, int numColumns) 151 { 152 // convenience matrix allocator for Cluster() 153 double[][] result = new double[k][]; 154 for (int i = 0; i < k; ++i) 155 result[i] = new double[numColumns]; 156 return result; 157 } 158 159 private static bool UpdateMeans(double[][] data, int[] clustering, double[][] means) 160 { 161 // returns false if there is a cluster that has no tuples assigned to it 162 // parameter means[][] is really a ref parameter 163 164 // check existing cluster counts 165 // can omit this check if InitClustering and UpdateClustering 166 // both guarantee at least one tuple in each cluster (usually true) 167 int numClusters = means.Length; 168 int[] clusterCounts = new int[numClusters]; 169 for (int i = 0; i < data.Length; ++i) 170 { 171 int cluster = clustering[i]; 172 ++clusterCounts[cluster]; 173 } 174 175 for (int k = 0; k < numClusters; ++k) 176 if (clusterCounts[k] == 0) 177 return false; // bad clustering. no change to means[][] 178 179 // update, zero-out means so it can be used as scratch matrix 180 for (int k = 0; k < means.Length; ++k) 181 for (int j = 0; j < means[k].Length; ++j) 182 means[k][j] = 0.0; 183 184 for (int i = 0; i < data.Length; ++i) 185 { 186 int cluster = clustering[i]; 187 for (int j = 0; j < data[i].Length; ++j) 188 means[cluster][j] += data[i][j]; // accumulate sum 189 } 190 191 for (int k = 0; k < means.Length; ++k) 192 for (int j = 0; j < means[k].Length; ++j) 193 means[k][j] /= clusterCounts[k]; // danger of div by 0 194 return true; 195 } 196 197 private static bool UpdateClustering(double[][] data, int[] clustering, double[][] means) 198 { 199 // (re)assign each tuple to a cluster (closest mean) 200 // returns false if no tuple assignments change OR 201 // if the reassignment would result in a clustering where 202 // one or more clusters have no tuples. 203 204 int numClusters = means.Length; 205 bool changed = false; 206 207 int[] newClustering = new int[clustering.Length]; // proposed result 208 Array.Copy(clustering, newClustering, clustering.Length); 209 210 double[] distances = new double[numClusters]; // distances from curr tuple to each mean 211 212 for (int i = 0; i < data.Length; ++i) // walk thru each tuple 213 { 214 for (int k = 0; k < numClusters; ++k) 215 distances[k] = Distance(data[i], means[k]); // compute distances from curr tuple to all k means 216 217 int newClusterID = MinIndex(distances); // find closest mean ID 218 if (newClusterID != newClustering[i]) 219 { 220 changed = true; 221 newClustering[i] = newClusterID; // update 222 } 223 } 224 225 if (changed == false) 226 return false; // no change so bail and don‘t update clustering[][] 227 228 // check proposed clustering[] cluster counts 229 int[] clusterCounts = new int[numClusters]; 230 for (int i = 0; i < data.Length; ++i) 231 { 232 int cluster = newClustering[i]; 233 ++clusterCounts[cluster]; 234 } 235 236 for (int k = 0; k < numClusters; ++k) 237 if (clusterCounts[k] == 0) 238 return false; // bad clustering. no change to clustering[][] 239 240 Array.Copy(newClustering, clustering, newClustering.Length); // update 241 return true; // good clustering and at least one change 242 } 243 244 private static double Distance(double[] tuple, double[] mean) 245 { 246 // Euclidean distance between two vectors for UpdateClustering() 247 // consider alternatives such as Manhattan distance 248 double sumSquaredDiffs = 0.0; 249 for (int j = 0; j < tuple.Length; ++j) 250 sumSquaredDiffs += Math.Pow((tuple[j] - mean[j]), 2); 251 return Math.Sqrt(sumSquaredDiffs); 252 } 253 254 private static int MinIndex(double[] distances) 255 { 256 // index of smallest value in array 257 // helper for UpdateClustering() 258 int indexOfMin = 0; 259 double smallDist = distances[0]; 260 for (int k = 0; k < distances.Length; ++k) 261 { 262 if (distances[k] < smallDist) 263 { 264 smallDist = distances[k]; 265 indexOfMin = k; 266 } 267 } 268 return indexOfMin; 269 } 270 271 // misc display helpers for demo 272 273 static void ShowData(double[][] data, int decimals, bool indices, bool newLine) 274 { 275 for (int i = 0; i < data.Length; ++i) 276 { 277 if (indices) Console.Write(i.ToString().PadLeft(3) + " "); 278 for (int j = 0; j < data[i].Length; ++j) 279 { 280 if (data[i][j] >= 0.0) Console.Write(" "); 281 Console.Write(data[i][j].ToString("F" + decimals) + " "); 282 } 283 Console.WriteLine(""); 284 } 285 if (newLine) Console.WriteLine(""); 286 } 287 288 static void ShowVector(int[] vector, bool newLine) 289 { 290 for (int i = 0; i < vector.Length; ++i) 291 Console.Write(vector[i] + " "); 292 if (newLine) Console.WriteLine("\n"); 293 } 294 295 static void ShowClustered(double[][] data, int[] clustering, int k, int decimals) 296 { 297 for (int w = 0; w < k; ++w) 298 { 299 Console.WriteLine("==================="); 300 for (int i = 0; i < data.Length; ++i) 301 { 302 int clusterID = clustering[i]; 303 if (clusterID != w) continue; 304 Console.Write(i.ToString().PadLeft(3) + " "); 305 for (int j = 0; j < data[i].Length; ++j) 306 { 307 if (data[i][j] >= 0.0) Console.Write(" "); 308 Console.Write(data[i][j].ToString("F" + decimals) + " "); 309 } 310 Console.WriteLine(""); 311 } 312 Console.WriteLine("==================="); 313 } 314 } 315 } 316 }
本篇文章《K-Means 聚类算法》由 Dennis Gao 发表自博客园个人博客,未经作者本人同意禁止以任何的形式转载,任何自动的或人为的爬虫转载行为均为耍流氓。
标签:
原文地址:http://www.cnblogs.com/gaochundong/p/kmeans_clustering.html