标签:
根据输入的各个叶节点的权值,构建一棵最优树,根据最小带全路径,确定由0,1组成的哈弗曼编码。
首先在一个封装类TNode中构建一棵树的元素,比如权值,左节点,右节点,同时在TNode类中构建了哈弗曼编码值,以及判断节点是否为叶子节点
package 霍夫曼编码; /** * * @author luckid * @version 2014_10_11 * */ /** * 定义Huffman编码的节点 */ public class TNode { /** * * @param weight * @param left * @param right */ /*protected*/ int weight; //权值 TNode left=null; //左节点 TNode right=null; //右节点 String code=null; //霍夫曼编码 /** * 构造一个赫夫曼编码节点的实例。设定左右子树和权值 */ public TNode(int weight,TNode left,TNode right){ this.weight=weight; this.left=left; this.right=right; } /** * * @author 刘雁冰as * @date 2015-02-08 1943 * */ public TNode(int weight){ this.weight=weight; } /** * 判断本节点是否为叶子节点 * @return boolean 为叶子节点则返回true */ public boolean isLeaf(){ return (left==null&&right==null); } /** * 返回本节点的权值 * @return nt 本节点的权值 */ public int getWeight(){ return weight; } /** * 返回本节点的左孩子节点 * @return TNode 左孩子节点 */ public TNode getLeft(){ return left; } /** * 返回本节点的右孩子节点 * @return TNode 右孩子节点 */ public TNode getRight(){ return right; } /** * 设置节点的赫夫曼编码 * @param str String 被设置的赫夫曼编码 */ public void setCode(String str){ code=str; } /** * 得到节点的赫夫曼编码 * @return String 被设置的赫夫曼编码 */ public String getCode(){ return code; } }
在Tree类中,构建一棵最优树。首先从键盘读入权值,在这里用1,3,5,7作为测试数据,将读入的测试数据放在一个数组链表中。接着使用迭代器求出最小的叶子节点,然后递归构建一棵最优树,在建构最优树的时候,一次递归需要找出权值最小的叶子节点以及权值次小的叶子节点,两个节点构成一棵子最优树。循序渐进继续递归,直到数组链表中只剩下一个数据,作为整棵最优树的根节点。
测试数据构成的最优子树应该如下:
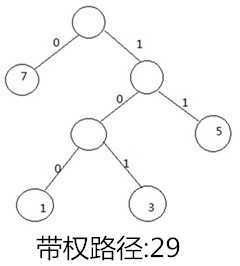
/** * 定义最优二叉树 */ /*protected*/ TNode root; //二叉树根节点 /*protected*/ List<Integer>leafList=new ArrayList<Integer>(); //存储叶子节点的权值 /*protected*/ List<TNode>tempList=new LinkedList<TNode>(); //临时队列,用于存放待组合的节点 /*protected*/TNode[]leafArr=null; //存放带权节点 /** * 键盘读取各个权值 */ public void getLeafWeight(){ Scanner sc=new Scanner(System.in); System.out.println("请输入各个叶节点的权值,按0为结束:"); while(sc.hasNextInt()){ int i=sc.nextInt(); if(i==0) break; leafList.add(new Integer(i)); } sc=null; return ; } /** * 找出临时队列中权值最小的节点从队列中移出并返回 * @return TNode 权值最小的节点 */ public TNode min(){ Iterator<TNode>iter=tempList.iterator(); TNode minNode=iter.next(); int min=minNode.getWeight(); //找到最小的节点 TNode tempNode; while(iter.hasNext()){ tempNode=iter.next(); if(tempNode.getWeight()<min){ min=tempNode.getWeight(); minNode=tempNode; } } tempList.remove(minNode); //最小的节点移出临时队列 //处理垃圾 iter=null; tempNode=null; return minNode; } /** * 根据权值创建叶子节点并加入临时队列 */ public void makeLeafNode(){ leafArr=new TNode[leafList.size()]; for(int i=0;i<leafList.size();i++){ TNode node=new TNode(leafList.get(i).intValue()); leafArr[i]=node; tempList.add(node); } } /** * 根据权值构造最优的二叉树 */ public void makeBestTree(){ makeLeafNode(); //根据权值创建叶子节点并加入临时队列 TNode minNode1=null; TNode minNode2=null; TNode node=null; while(tempList.size()!=1){ //构造最优树 minNode1=min(); minNode2=min(); node=new TNode(minNode1.getWeight()+minNode2.getWeight(),minNode1,minNode2); tempList.add(node); } root=node; }
构建好了最优树,就可以用HuffmanCode类拓展最优二叉树实现哈弗曼编码。在HuffmanCode类中递归调用huff()方法创建哈弗曼树结构,并且为每个叶子节点赋值,其中左子树赋值0,右子树赋值1
package 霍夫曼编码; /** * * @author 刘雁冰as * @date 2015-02-08 1943 * */ /** * 拓展最优二叉树实现Huffman编码 * 赫夫曼编码类 */ public class HuffmanCode extends Tree{ public HuffmanCode(){ init(); } /** * 初始化节点值并构造最优二叉树 */ public void init(){ super.getLeafWeight(); super.makeBestTree(); } /** * 生成赫夫曼编码的递归函数 * * @param t TNode 当前遍历节点 * @param s String 目前遍历至此的赫夫曼编码 */ /*protected*/public void huff(TNode t,String s){ if(t.isLeaf()){ t.setCode(s); } else{ huff(t.left,s+"0"); huff(t.right,s+"1"); } } /** * 生成赫夫曼编码的外部调用函数 */ public void makeHuffmanCode(){ huff(root,""); } /** * 查看所有的赫夫曼编码值 */ public void viewHuffmanCode(){ for(int i=0;i<leafArr.length;i++){ System.out.println(leafArr[i].weight+":"+leafArr[i].getCode()); } } }
测试类:
package 霍夫曼编码; public class Application { /** * * @author 刘雁冰as * @date 2015-02-08 1943 * */ public static void main(String args[]){ // TODO Auto-generated method stub HuffmanCode hu=new HuffmanCode(); hu.makeHuffmanCode(); hu.viewHuffmanCode(); } }
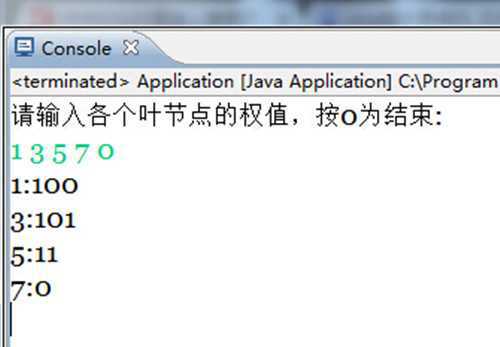
测试结果如下:
标签:
原文地址:http://www.cnblogs.com/luckid/p/4280379.html