POJ 2029 Get Many Persimmon Trees (二维树状数组 or DP)

标签：

题意：一个H * W的大矩形，里面的某些格子种有树。现在要你找出一个h * w的小矩形，使得里面树的数量最多，问最多有多少棵树

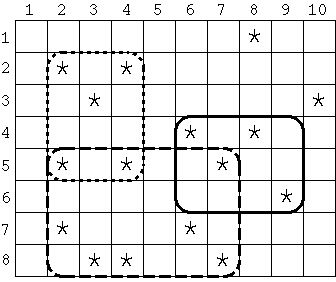
是二维树状数组基础用法，边输入边更新有树的点，建完树后就可以查询每个（1，1）到（x,y）为对顶点的矩形中共有多少棵柿子树。

算法复杂度 O(H*W*lgH*lgW)

但是由于这题的柿子树一旦确定位置后就没有更新位置，所以不需要用树状数组也可，直接用dp统计每个（1，1）到（x,y）为对顶点的矩形中共有多少棵柿子树。

统计的状态转移方程是：

        for(int i=1;i<=hig;i++)
        for(int j=1;j<=wid;j++)
            dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+dp[i][j];

总算法复杂度是O(H*W)比用树状数组更优

树状数组代码：

//180K	16MS
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define M 100+10
int tree[M][M];
int m,wid,hig;
int lowbit(int x){return x&-x;}

void update(int x,int y)
{
    while(y<=hig){
        int tmp=x;
        while(tmp<=wid){
            tree[y][tmp]++;
            tmp+=lowbit(tmp);
        }
        y+=lowbit(y);
    }
}
int query(int x,int y)
{
    int s=0;
    while(y>0){
        int tmp=x;
        while(tmp>0){
            s+=tree[y][tmp];
            tmp-=lowbit(tmp);
        }
        y-=lowbit(y);
    }
    return s;
}
int main()
{
    while(scanf("%d",&m),m){
        memset(tree,0,sizeof(tree));
        scanf("%d%d",&wid,&hig);
        for(int i=1;i<=m;i++){
            int x,y;
            scanf("%d%d",&x,&y);
            update(x,y);
        }
        int w,h;
        scanf("%d%d",&w,&h);
        int ans=-1;
        for(int i=1;i<=hig;i++)
        for(int j=1;j<=wid;j++){
            if(j+w-1>wid||i+h-1>hig) continue;
            int cnt= query(j+w-1,i+h-1)-query(j+w-1,i-1)-query(j-1,i+h-1)+query(j-1,i-1);
            ans=max(ans,cnt);
        }
        printf("%d\n",ans);
    }
    return 0;
}

DP代码：

//180K	0MS
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define M 100+10
int dp[M][M];
int m,wid,hig;
int main()
{
    while(scanf("%d",&m),m){
        memset(dp,0,sizeof(dp));
        scanf("%d%d",&wid,&hig);
        for(int i=1;i<=m;i++){
            int x,y;
            scanf("%d%d",&x,&y);
            dp[y][x]=1;
        }
        for(int i=1;i<=hig;i++)
        for(int j=1;j<=wid;j++)
            dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+dp[i][j];

        int w,h;
        scanf("%d%d",&w,&h);
        int ans=-1;
        for(int i=1;i<=hig;i++)
        for(int j=1;j<=wid;j++){
            if(j+w-1>wid||i+h-1>hig) continue;
            int cnt= dp[i+h-1][j+w-1]-dp[i+h-1][j-1]-dp[i-1][j+w-1]+dp[i-1][j-1];
            ans=max(ans,cnt);
        }
        printf("%d\n",ans);
    }
    return 0;
}

POJ 2029 Get Many Persimmon Trees (二维树状数组 or DP)

标签：

原文地址：http://blog.csdn.net/kalilili/article/details/43912747