标签:
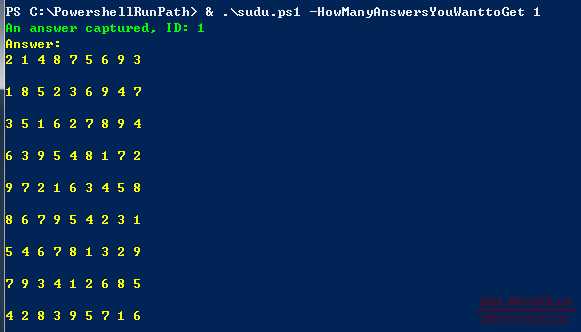
Sudoku is a numbers filling game, most known by people is 9x9 class, the algorithm is using confirmed numbers to get all possible numbers for each cell, if the number if possible numbers for a cell is 1, then the cell value confirmed, if greater or equal than 2, script makes loop and calculates a potential answer. Since answers are not unique, so a parameter is added to specify how many answers to return.
param(
# 返回几个答案
[int]$HowManyAnswersYouWanttoGet = 1
)
$SudokuMatrix = @(
@(0,0,0, 0,0,0, 0,0,3),
@(0,0,0, 0,0,0, 0,4,0),
@(0,5,1, 6,0,0, 0,0,0),
@(0,3,0, 0,0,8, 0,0,2),
@(9,0,0, 1,6,0, 0,0,0),
@(0,6,0, 0,5,4, 0,0,0),
@(5,4,0, 0,0,0, 0,2,0),
@(0,0,3, 4,0,2, 0,0,0),
@(0,0,8, 3,0,0, 7,1,0)
)
# Loop each cell, add array [1..9] for each null cell.
for($i = 0; $i -lt 9; $i++){
for($j = 0; $j -lt 9; $j++){
if(!$SudokuMatrix[$i][$j]){
$SudokuMatrix[$i][$j] = 1..9
}else{
$SudokuMatrix[$i][$j] = @($SudokuMatrix[$i][$j])
}
}
}
# Loop each cell, calculate possible numbers to remove impossible numbers for the cell.
function GoLoop($arr){
$NewArr = @($null) * 9
for($i = 0; $i -lt 9; $i++){
$NewArr[$i] = $arr[$i].PSObject.Copy()
}
for($i = 0; $i -lt 9; $i++){
for($j = 0; $j -lt 9; $j++){
if($NewArr[$i][$j].Count -ne 1){
for($k = 0; $k -lt 9; $k++){
if($NewArr[$i][$k].Count -eq 1 -and $NewArr[$i][$j].Count -ne 1){
$NewArr[$i][$j] = @($NewArr[$i][$j] | ?{$_ -ne $NewArr[$i][$k][0]})
}
if($NewArr[$k][$j].Count -eq 1 -and $NewArr[$i][$j].Count -ne 1){
$NewArr[$i][$j] = @($NewArr[$i][$j] | ?{$_ -ne $NewArr[$k][$j][0]})
}
}
}
}
}
return $NewArr
}
# Loop each cell, if the possible number of the cell is null, means current calculation is wrong.
function VerifyZero($arr){
for($i = 0; $i -lt 9; $i++){
for($j = 0; $j -lt 9; $j++){
if($arr[$i][$j].Count -eq 0){
return $i, $j, $true
}
}
}
return $i, $j, $false
}
# Find the most less of possible numbers for a cell, return the position.
function FindSmallest($arr){
foreach($k in 2..9){
for($i = 0; $i -lt 9; $i++){
for($j = 0; $j -lt 9; $j++){
if($arr[$i][$j].Count -eq $k){
return $i, $j, $k
}
}
}
}
}
# Calculate how many cells have been confirmed, if it‘s 81, correct answer hit.
function CountConfirmedNumber($arr){
$NumberConfirmed = 0
for($i = 0; $i -lt 9; $i++){
for($j = 0; $j -lt 9; $j++){
if($arr[$i][$j].Count -eq 1){
$NumberConfirmed++
}
}
}
return $NumberConfirmed
}
$AnswerCount = 0
$Results = @()
function GoCalculate($arr){
$NewArray = GoLoop($arr)
# verify no zero option!
$ZeroPosition = VerifyZero($NewArray)
if($ZeroPosition[2]){
# Write-Host "0 option found: [$($ZeroPosition[0])][$($ZeroPosition[1])]"
return
}
# confirm current numbers
if((CountConfirmedNumber($NewArray)) -eq 81){
$Script:AnswerCount++
Write-Host "An answer captured, ID: $AnswerCount" -ForegroundColor Green
# Write-Host "81 numbers confirmed."
$Script:Results += $null
$Script:Results[-1] = $NewArray
return
}
# find the nearest(to [0][0]) and smallest(2 to 9) option element.
$Smallest = FindSmallest($NewArray)
$OptionsStack = @($NewArray[$Smallest[0]][$Smallest[1]])
# Write-Host "Row: $($Smallest[0]); Col: $($Smallest[1]); Option: $($OptionsStack -join ‘ ‘)"
foreach($Option in $OptionsStack){
# Write-Host "Set [$($Smallest[0])][$($Smallest[1])] to: $Option"
$NewArray[$Smallest[0]][$Smallest[1]] = @($Option)
if($AnswerCount -lt $HowManyAnswersYouWanttoGet){
GoCalculate($NewArray)
}
}
}
# Trigger
GoCalculate($SudokuMatrix)
# Output answers
$Results | %{
if($_ -eq $null){return}
Write-Host "Answer:" -ForegroundColor Yellow
for($i = 0; $i -lt 9; $i++){
for($j = 0; $j -lt 9; $j++){
Write-Host "$($_[$i][$j][0]) " -NoNewline -ForegroundColor yellow
}
Write-Host "`n"
}
}
[Powershell] An algorithm to 9x9 sudoku.
标签:
原文地址:http://www.cnblogs.com/LarryAtCNBlog/p/4307965.html