二十世纪最有影响力的十大算法之一：蒙特卡洛方法

时间：2015-03-03 20:35:22 阅读：300 评论：0 收藏：0 [点我收藏+]

标签：

第一部分：算法介绍

[1946: John von Neumann, Stan Ulam, and Nick Metropolis, all at the Los Alamos Scientific Laboratory, cook up the Metropolis algorithm, also known as the Monte Carlo method.]1946年，美国拉斯阿莫斯国家实验室的三位科学家John von Neumann,Stan Ulam 和 Nick Metropolis共同发明，被称为蒙特卡洛方法。它的具体定义是：在广场上画一个边长一米的正方形，在正方形内部随意用粉笔画一个不规则的形状，现在要计算这个不规则图形的面积，怎么计算列?蒙特卡洛(Monte Carlo)方法告诉我们，均匀的向该正方形内撒N（N 是一个很大的自然数）个黄豆，随后数数有多少个黄豆在这个不规则几何形状内部，比如说有M个，那么，这个奇怪形状的面积便近似于M/N，N越大，算出来的值便越精确。在这里我们要假定豆子都在一个平面上，相互之间没有重叠。(撒黄豆只是一个比喻。)

第二部分：算法特点

蒙特卡洛方法的伟大之处，在于对精确性问题无法解决的时候，利用“穷举”的思想来模拟求解。在各个领域得以应用。本质是模拟（simulation）：利用大量随机输入，产生各种输出；结果的概率分布就是真实分布的“近似”。所以，输入的分布是否随机（目前计算机所能做的就是伪随机，并不能产生真正的随机分布），输入的量是否足够，这个过程我们成为Sampling Random Variables，决定是否能“近似”的关键。这往往和应用有关系。

第三部分：应用和实践

实践：计算机圆周率

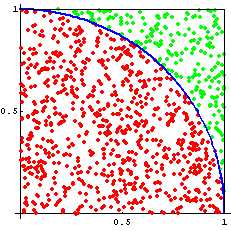
蒙特卡洛方法可以用于产生接近pi的近似值。下图显示了一个带有1/4圆在内的正方形单元、落在圈内（红点）的点和总的投在正方形（红和绿点）上的点的比率为：pi/4。这一过程称为使用蒙特卡洛方法来仿真逼近pi实际值。

技术分享

java实现：

 1 import java.util.Random;
 2 public class PiSimulation {
 3  
 4  private static Random rnd = new Random();
 5  public static void main(String args[])
 6  {
 7   //simulate pi
 8   int iter = 10000*10000;//0.1billion
 9   int totalIn = 0;
10   for(int i=0;i<iter;i++)
11   {
12    double x = rnd.nextDouble();
13    double y = rnd.nextDouble();
14    if(inCircle(x, y))
15     totalIn++;
16   }
17   System.out.println("simulate pi:"+((double)totalIn/iter*4));
18  
19  }
20  
21  public static boolean inCircle(double x,double y)//是否在1/4圆范围之内
22  {
23   if((x*x+y*y)<=1)
24    return true;
25   return false;
26  }
27 }
28 
29 simulate pi:3.14143168