标签:
树状数组(Binary Indexed Tree(BIT), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有
元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素的值。
这种数据结构(算法)并没有C++和Java的库支持,需要自己手动实现。在Competitive Programming的竞赛中被广泛的使用。树状数组
和线段树很像,但能用树状数组解决的问题,基本上都能用线段树解决,而线段树能解决的树状数组不一定能解决。相比较而言,树状数组
效率要高很多。但使用范围比线段树小(如查询每个区间最小值问题需要线段树)。
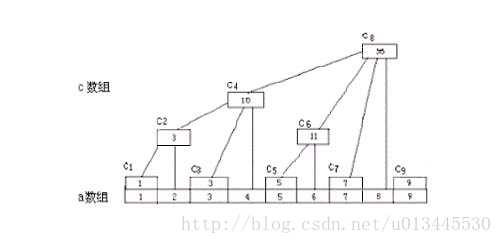
分析上面的几组式子可知,当 i 为奇数时,ci=ai ;当 i 为偶数时,就要看 i 的因子中最多有二的多少次幂,
例如,6 的因子中有 2 的一次幂,等于 2 ,所以 c6=a5+a6(由六向前数两个数的和),4 的因子中有 2 的两次幂,等于 4
所以 c4=a1+a2+a3+a4(由四向前数四个数的和)。
1 /*树状数组模板题*/ 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #define MAXN 50005 6 using namespace std; 7 int que[MAXN],c[MAXN]; 8 char chr[10]; 9 int lowbit(int x) 10 { 11 return x&(-x);//用来计算a^k中的k 12 } 13 void create(int n) 14 { 15 int i,s,j; 16 for(i=1;i<=n;i++) 17 { 18 s=lowbit(i); 19 // cout<<s<<endl; 20 for(j=0;j<s;j++) 21 { 22 c[i]=c[i]+que[i-j]; 23 } 24 } 25 // for(i=1;i<=n;i++) 26 // cout<<c[i]<<endl; 27 } 28 //求数组的和的算法如下 29 int sum(int n) 30 { 31 int s=0; 32 while(n>0) 33 { 34 s+=c[n]; 35 n=n-lowbit(n); 36 } 37 return s; 38 } 39 void change(int i,int n,int x) 40 { 41 while(i<=n) 42 { 43 c[i]=c[i]+x; 44 i=i+lowbit(i); 45 } 46 } 47 int main() 48 { 49 int t,cas=1,i,j,n,x,s,a,b; 50 cin>>t; 51 while(t--) 52 { 53 memset(c,0,sizeof(c)); 54 cin>>n; 55 for(i=1;i<=n;i++) 56 scanf("%d",&que[i]); 57 create(n); 58 cout<<"Case "<<cas++<<":"<<endl; 59 while(1) 60 { 61 scanf("%s",chr); 62 if(!strcmp(chr,"Add")) 63 { 64 cin>>j>>x; 65 change(j,n,x); 66 } 67 else if(!strcmp(chr,"Sub")) 68 { 69 cin>>j>>x; 70 change(j,n,-x); 71 } 72 else if(!strcmp(chr,"Query")) 73 { 74 cin>>a>>b; 75 //cout<<sum(b)<<sum(a-1)<<endl; 76 s=sum(b)-sum(a-1); 77 cout<<s<<endl; 78 } 79 else 80 break; 81 } 82 } 83 return 0; 84 }
标签:
原文地址:http://www.cnblogs.com/fancy-itlife/p/4312170.html