弗洛伊德(Floyd)算法

  1 #include <stdio.h>
  2 
  3 #define MAXVEX 20        //最大顶点数
  4 #define INFINITY 65535    //∞
  5 
  6 
  7 typedef struct
  8 {/*    图结构    */
  9     int vexs[MAXVEX];//顶点下标
 10     int arc[MAXVEX][MAXVEX];//矩阵
 11     int numVertexes, numEdges;//顶点数和边数
 12 }MGraph;
 13 
 14 //用户定义类型
 15 typedef int Patharc[MAXVEX][MAXVEX];
 16 typedef int ShortPathTable[MAXVEX][MAXVEX];
 17 
 18 void CreateMGraph(MGraph *G)
 19 {/*    创建图    */
 20     int i, j;
 21 
 22     //printf ("请输入顶点数和边数");
 23     //提前输入
 24     G->numVertexes = 9;
 25     G->numEdges = 16;
 26 
 27     //初始化顶点下标
 28     for(i=0; i<G->numVertexes; i++)
 29         G->vexs[i] = i;
 30 
 31     //初始化矩阵
 32     for(i=0; i<G->numVertexes; i++)
 33         for(j=0; j<G->numVertexes; j++)
 34             if(i == j)
 35                 G->arc[i][j] = 0;
 36             else
 37                 G->arc[i][j] = INFINITY;
 38 
 39     //提前手动输入权值
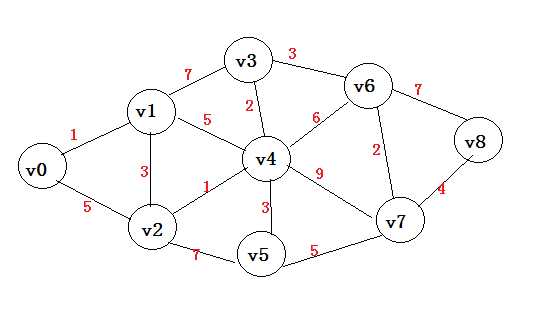
 40     G->arc[0][1] = 1;
 41     G->arc[0][2] = 5; 
 42 
 43     G->arc[1][2] = 3; 
 44     G->arc[1][3] = 7; 
 45     G->arc[1][4] = 5; 
 46 
 47     G->arc[2][4] = 1; 
 48     G->arc[2][5] = 7; 
 49 
 50     G->arc[3][4] = 2; 
 51     G->arc[3][6] = 3; 
 52 
 53     G->arc[4][5] = 3;
 54     G->arc[4][6] = 6;
 55     G->arc[4][7] = 9; 
 56 
 57     G->arc[5][7] = 5; 
 58 
 59     G->arc[6][7] = 2; 
 60     G->arc[6][8] = 7;
 61 
 62     G->arc[7][8] = 4;
 63 
 64     //矩阵上三角对称下三角
 65     for(i=0; i<G->numVertexes; i++)
 66         for(j=i; j<G->numVertexes; j++)
 67             G->arc[j][i] = G->arc[i][j];
 68 
 69     return;
 70 }
 71 
 72 void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D)
 73 {/*    D数组用于存储最短路径的权值，P数组用于存储最短路径经过顶点的下表    */
 74     int v, w, k;
 75     
 76     //初始化D与P
 77     for(v=0; v<G.numVertexes; v++)
 78         for(w=0; w<G.numVertexes; w++)
 79         {
 80             (*D)[v][w] = G.arc[v][w];//D[v][w]值即为对应的权值
 81             (*P)[v][w] = w;//初始化P
 82         }
 83 
 84     for(k=0; k<G.numVertexes; k++)
 85         for(v=0; v<G.numVertexes; v++)
 86             for(w=0; w<G.numVertexes; w++)
 87                 if((*D)[v][w] > (*D)[v][k]+(*D)[k][w])
 88                 {//这里可以理解为：v到w 的路径比 v到k 然后 k到w 的路径，目的是要v顶点到达w顶点，然后采取间接的方法进行比较
 89                     (*D)[v][w] = (*D)[v][k] + (*D)[k][w];//经过顶点k比直达更近，则赋值
 90                     (*P)[v][w] = (*P)[v][k];//经过顶点的下表赋给对应的P数组        
 91                 }//v代表起始顶点的下表，k代表中转顶点的下表，w代表终点顶点的下表
 92 
 93     return;
 94 }
 95 
 96 int main(void)
 97 
 98 {
 99     int v, w, k;
100     
101     MGraph G;
102 
103     Patharc P;//定义存储最短路径经过的顶点下标的数组
104     ShortPathTable D;//定义存储各点最短路径
105 
106     CreateMGraph(&G);//创建图
107 
108     ShortestPath_Floyd(G, &P, &D);//最短路径——弗洛伊德
109 
110     printf("\t\t\t各顶点最短路径如下：\n");
111     for(v=0; v<G.numVertexes; v++)
112     {
113         for(w=v+1; w<G.numVertexes; w++)
114         {
115             printf("v%d-v%d weight:%d\t", v, w, D[v][w]);//顶点—》顶点——权值
116             k = P[v][w];//经过顶点下标
117             printf("path:%d", v);//打印源点
118             while(k != w)
119             {//若经过顶点不等于终点
120                 printf(" ->%d", k);//则打印经过顶点
121                 k = P[k][w];//        获取下一个经过顶点
122             }
123             printf(" ->%d\n", w);
124         }
125         printf("\n");
126     }
127 
128     printf("\t\t\t最短路径D：\n");
129     for(v=0; v<G.numVertexes; v++)
130     {
131         for(w=0; w<G.numVertexes; w++)
132             printf("%5d", D[v][w]);
133         printf("\n");
134     }
135 
136     printf("\t\t\t最短路径P：\n");
137     for(v=0; v<G.numVertexes; v++)
138     {
139         for(w=0; w<G.numVertexes; w++)
140             printf("%5d", P[v][w]);
141         printf("\n");
142     }
143 
144     return 0;
145 }