标签:
本文介绍使用深度先搜索对向无环图(DAG)进行拓扑排序。
对于一个有向无环图G=(V,E)来说,其拓扑排序是G中所有结点的一种线性次序,该次序满足如下条件:如果G包含边(u,v)则结点u在拓扑排序中处于结点v的前面(若图G包含一个环路则不可能排出一个线性次序)。可将图中的拓扑排序看成是将图的所有结点在一条水平线上排开,图中所有边都从左指向右。
给一个拓扑图如下示:
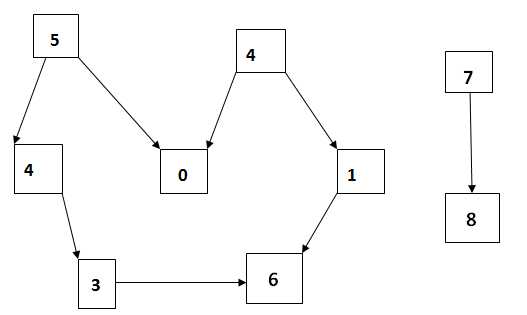
拓扑排序算法与DFS相似,但是在拓扑排序的过程中,每个结点都是后与其临接链表里的结点而放入Stack中。
具体代码如下示:
1 #include <iostream> 2 #include <list> 3 #include <stack> 4 using namespace std; 5 6 //拓扑排序里的图应该是有向无环图 7 class DAG{ 8 private: 9 int v; 10 list<int> *adj; 11 void topologicalSortUtil(int v,bool *visited,stack<int>& Stack); 12 public: 13 DAG(int v);//ctor 14 void addEdge(int start,int end);//DAG中是有向图 15 void topologicalSort(); 16 }; 17 18 DAG::DAG(int v){ 19 this->v = v; 20 adj = new list<int>[v]; 21 } 22 23 void DAG::addEdge(int start,int end){ 24 adj[start].push_back(end); 25 } 26 27 void DAG::topologicalSortUtil(int v,bool* visited,stack<int>& Stack){ 28 visited[v] = true; 29 30 list<int>::iterator beg = adj[v].begin(); 31 for (;beg != adj[v].end();++beg) 32 if (visited[*beg] == false) 33 topologicalSortUtil(*beg,visited,Stack); 34 Stack.push(v); 35 } 36 37 void DAG::topologicalSort(){ 38 stack<int> Stack = stack<int>(); 39 bool *visited = new bool[v]; 40 for (int i=0;i<v;i++) 41 visited[i] = false; 42 43 //recursive call tsutil function to store TopoligicalSort 44 //one by one 45 for (int i=0;i<v;i++) 46 if (visited[i] == false) 47 topologicalSortUtil(i,visited,Stack); 48 49 while(!Stack.empty()){ 50 cout<<Stack.top()<<" "; 51 Stack.pop(); 52 } 53 } 54 55 int main(){ 56 DAG dag = DAG(9); 57 dag.addEdge(1,6); 58 dag.addEdge(2,3); 59 dag.addEdge(3,6); 60 dag.addEdge(4,0); 61 dag.addEdge(4,1); 62 dag.addEdge(5,2); 63 dag.addEdge(5,0); 64 dag.addEdge(5,1); 65 dag.addEdge(7,8); 66 67 cout<<"Topological Sort of the given Directed Acyclic Graph(DAG): "<<endl; 68 dag.topologicalSort(); 69 cout<<endl; 70 71 return 0; 72 }
运行结果为:

文献引用:算法导论->22.4拓扑排序
代码参考:http://www.geeksforgeeks.org/topological-sorting/
标签:
原文地址:http://www.cnblogs.com/lxiao/p/4321020.html