标签:
归并排序的核心思想是将两个已经排序的序列合并成一个序列,那如何得到两个已经排序的序列呢?我们知道, 如果一个序列只有一个元素,那该序列是已经排序的,这样我们就可以利用分治的思想,将未排序的序列划分成更小的序列,只到我们可以很方便的对小序列进行排序(比如划分到序列只有一个元素, 或者序列很小可以方便的使用其它排序算法进行排序),然后再将小序列逐次合并,得到最后的排序结果。
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int num =0;
void merge(int in[], int out[], int l, int m, int r)
{
int i = l;
int k = m + 1;
while (l <= m && k <= r)
{
if (in[l] <= in[k]) {
out[i++] = in[l++];
}
else
{
out[i++] = in[k++];
/* 因为此时in[l...m]已经排序,如果in[l] 与 in[k] 逆序,
则in[l+1], in[l+2]...in[m] 都与in[k]逆序, 共 m-l+1 对*/
num += m - l + 1; /* calculate the inversion number */
}
}
while (l <= m) {
out[i++] = in[l++];
}
while (k <= r) {
out[i++] = in[k++];
}
}
/*
* @brief 递归将序列划分为只有一个元素的子序列, 然后逐次对子序列进行合并
*/
void m_sort(int in[], int out[], int l, int r)
{
/* 仅有一个元素, 已排序, 递归结束 */
if (l >= r) {
return;
}
/* 计算 l 和 r 的中间值, 防止溢出 */
int m = (l & r) + ((l ^ r) >> 1);
/* note that in and out are swapped */
m_sort(out, in, l, m);
m_sort(out, in, m + 1, r);
merge(in, out, l, m, r);
}
/*
* @brief merge sort
* 统一申请空间, 避免反复申请释放
*/
int merge_sort(int a[], int n)
{
int *b = (int *)malloc(n * sizeof(int));
if (b) {
memcpy(b, a, n * sizeof(int));
m_sort(b, a, 0, n - 1);
free(b);
return 0;
}
return -1;
}
int main()
{
int a[9]={2,1,3,8,5,7,4,6,10};
merge_sort(a,9);
for(int i=0;i<9;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}
这是一个递归算法,这个算法的理解其实可以借助下面这个图:
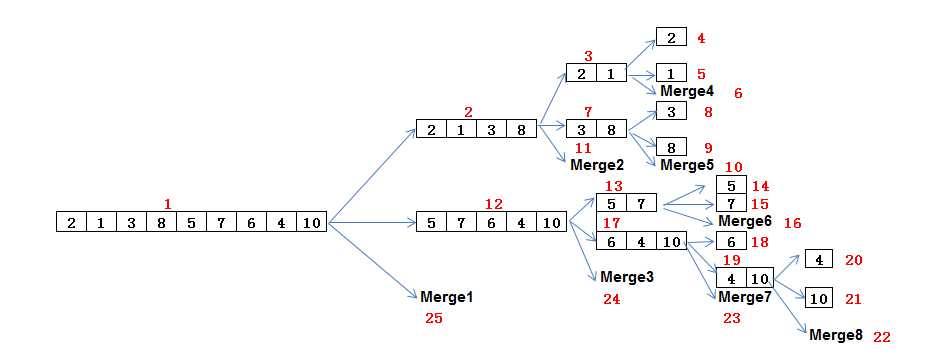
对于原始的数组2,1,3,8,5,7,6,4,10,在整个过程执行的是顺序是途中红色编号1-20。虽然我们描述中说的是程序先分解,再归并,但实际过程是一边分解一边归并,前半部分分先排好序,后半部分再拍好,最后整个归并为一个完整的序列,途中的merge过程它所在层的两个序列的merge过程:下图展示了每个merge过程对作用于数组的哪部分(红色)。
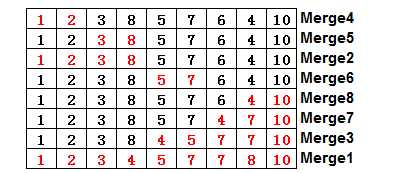
整个过程就像一个动态的树,执行顺序就是对树的先序遍历顺序。
最后实验验证,对10000个倒序的数组进行排序,直接插入排序需1024ms,二归并排序只需20ms。
归并排序详解
标签:
原文地址:http://blog.csdn.net/u014082714/article/details/44132111

