标签:
复习串的朴素模式匹配算法
模式匹配 :
子串定位运算,在主串中找出子串出现的位置。
在串匹配中,将主串 S 称为目标(串),子串 T 称为模式(串)。如果在主串 S 中能够找到子串 T, 则称匹配成功,返回 第一个 和 子串 T 中 第一个字符 相等 的 字符 在主串 S 中的 序号,否则,称匹配失败,返回 0。
算法思想:
从主串 S 的第 pos 个字符起和模式 T 的第一个字符比较之,若相同,则两者顺次的去比较后续的每一个字符,否则从主串 S 的下一个字符起再重新和模式 T 的字符比较之。 (为什么说它朴素,就是因为笨,因子串和主串的每躺比较,当发现匹配不对,则主串的指针要回溯到上次开始比较的字符处的下一个字符处,去重新比一遍!费劲)。
详细图解;
给定两个字符串,S 和 T,长度已知。
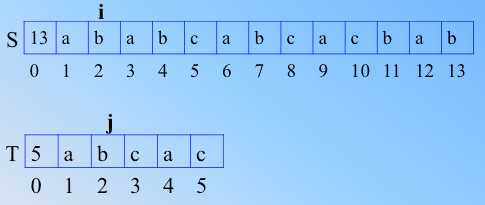 -》
-》 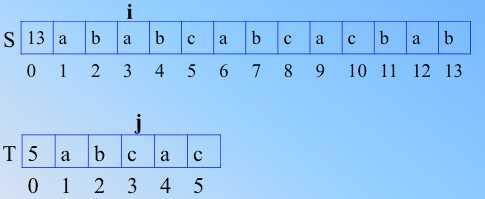
初始 ab 相同,可以顺次比较,当3处,不匹配。则j 回溯到T1处,i 回到S 的下一个字符 S2处,从新开始和 T1比较。
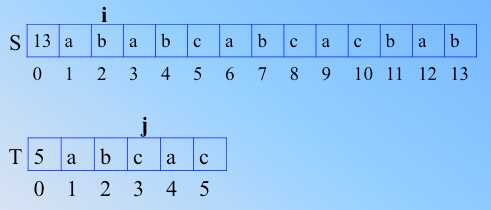 -》
-》 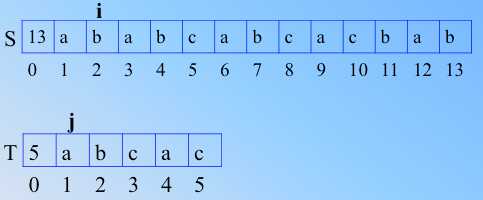
b 和 a又不匹配,j 回到1处(位置不变),i 回到下一个字符,也就是3处,继续比,匹配,顺次比较之。直到下面;
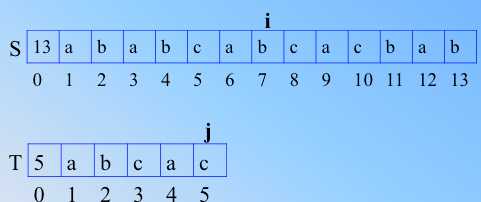

模式串的 j再次回溯到1,i 到4,继续比较,不匹配,T 的 j 继续回溯1,S的 i 继续到下一个字符,继续比较,直到 i=6,匹配
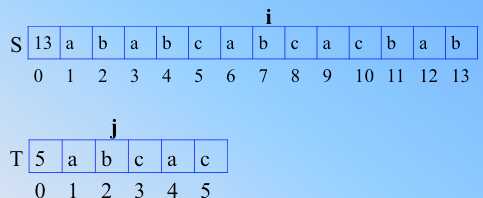
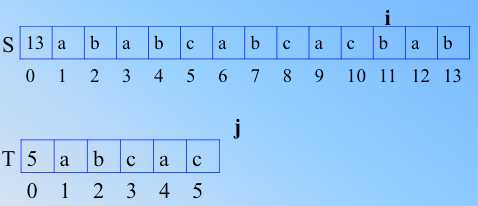
继续顺次比较,直到 T 比完,也就是在 j=5,i=10之后,j、i 继续++的时候,要判断出比完了,如图。这是整个过程。算法重要的是思想,理解思想,是第一步,脑子里有清晰的思路和完美的情景再现,那么代码实现都是水到渠成的事情。
用代码编写如下:
1 int getLength(char *str) 2 { 3 int i = 0; 4 5 while (‘\0‘ != str[i]) { 6 i++; 7 } 8 9 return i; 10 } 11 12 int strCompare(char *strMain, char *strSub, int index) 13 { 14 int iMain = index; 15 int jSub = 0; 16 int lenMain = getLength(strMain); 17 int lenSub = getLength(strSub); 18 19 while ((iMain >= 0 && iMain <= lenMain - 1) && ((jSub >= 0 && jSub <= lenSub - 1))){ 20 if (strMain[iMain] == strSub[jSub]) { 21 iMain++; 22 jSub++; 23 }else{ 24 iMain = iMain - jSub + 1;//回到主串的下一个位置起,开始比较,每次重新开始顺次比较, ij 走的长度是一样的,如果从0开始,那么相减之后,故+1到下一位,如果是从1开始存,那么+2到下一位。 25 jSub = 0; 26 } 27 } 28 //如果匹配 ok,肯定子串先比完。 29 if (jSub > lenSub - 1) { 30 return iMain - lenSub;//得到的就是匹配 ok 后,主串里第一个和模式串第一个字符匹配的字符的位置 31 }else{ 32 return 0;//匹配失败 33 } 34 } 35 36 int main(int argc, const char * argv[]) { 37 char *str1 = "sawtsafvda"; 38 char *str2 = "safv"; 39 40 int i = strCompare(str1, str2, 0); 41 42 printf("%d\n", i); 43 44 return 0; 45 }
4
Program ended with exit code: 0
分析时间复杂度
最坏的时候,最后匹配成功,比如,0000000000001 和 00001 ,比较每次都在00001的1开始不匹配,指针回溯到开头,主串也回溯 i-j+1,若模式子串的长度是m,目标串的长度是n,这时最坏的情况是每遍比较都在最后出现不等,即每遍最多比较m次,最多比较n-m+1遍,总的比较次数最多为m(n-m+1),因此朴素的模式匹配算法为 o(m*n),虽然,朴素的模式匹配,时间复杂度比较大,但是实际中,一般情况(除非模式串和主串之间存在很多的部分匹配的时候,因为此时每遍需要比较的次数很多,相乘不能近似),真正的执行时间是近似于o(n+m )的,故当今仍然有他的用处!
标签:
原文地址:http://www.cnblogs.com/kubixuesheng/p/4322410.html