标签:
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序的基本思想
综上可知:
归并排序其实要做两件事:
(1)“分解”——将序列每次折半划分。
(2)“合并”——将划分后的序列段两两合并后排序。
递归代码:
/**
* 归并排序
* @param a 待排序的数组
*/
public static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] a){
mergeSort(a,0,a.length-1);
}
/**
* 算法描述:如果N=1,不需要排序;否则递归地将前半部分和后半部分排序
* @param a 待排序的数组
* @param left 左边界
* @param right 右边界
*/
private static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] a,int left,int right){
if(left<right){
int mid = (left+right)/2;
mergeSort(a,left,mid);
mergeSort(a,mid+1,right);
merge(a,left,mid,right);
}
}
/**
* 将排好序的数组进行合并的操作过程
* @param a 待排序的数组
* @param left 左边界起点
* @param mid 左边界终点
* @param right 右边界终点
*/
private static <AnyType extends Comparable<? super AnyType>> void merge(AnyType[] a,int left,int mid,int right){
AnyType[] temp = (AnyType[]) new Comparable[right-left+1];
int tempPos = 0;
int rightStart = mid+1;
while(left <= mid&& rightStart<=right){
if(a[left].compareTo(a[rightStart])<0){
temp[tempPos++]=a[left++];
}else{
temp[tempPos++]=a[rightStart++];
}
}
while(left<=mid){
temp[tempPos++]=a[left++];
}
while(rightStart<=right){
temp[tempPos++]=a[rightStart++];
}
for(int i=temp.length-1;i>=0;i--,right--)
a[right]=temp[i];
}
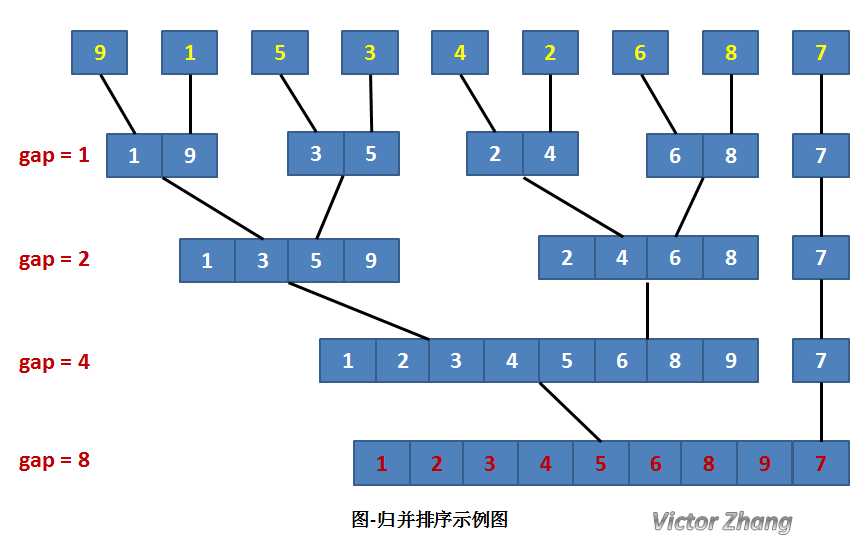
非递归的思路:以gap为一组数据的长度,[0,gap-1],[gap,2*gap-1]...令gap从1开始(每次gap<<1),每2组进行合并,从图中看即为从上之下的过程,
期间会出现以下情况:
i+2*gap-1<a.length 剩余元素不足两组,分为:
情形1:i+gap-1<length,剩余元素为1组+一点,继续合并[i,i+gap-1],[i+gap,length-1]
情形2;:i+gap-1>length,剩余元素不够1组,什么都不做(在gap扩大的时候会与前面的序列进行合并)
代码如下;
/**
* 非递归的方法
* @param a
*/
public static <AnyType extends Comparable<? super AnyType>> void mergeSort2(AnyType[] a){
//每次对相邻的gap进行排序
for(int gap=1;gap<a.length;gap=gap<<1){
mergeSort2(a,gap);
print(a);
}
}
private static <AnyType extends Comparable<? super AnyType>> void mergeSort2(AnyType[] a,int gap){
int i;
for(i=0;i+2*gap-1<a.length;i+=gap*2){
merge(a,i,(2*i+2*gap-1)/2,i+2*gap-1);
}
//还有可能存在剩余元素
//情形1:i+gap-1<length,剩余元素为1组+一点,继续合并
if(i+gap-1<a.length){
merge(a,i,i+gap-1,a.length-1);
}
//情形2:i+gap-1>length,剩余元素不够1组,什么都不做
}
测试的代码:
public static void main(String[] args) {
Integer a[] = new Integer[10];
for(int i =9;i>=0;i--)
a[9-i] = i;
print(a);
// insertionSort(a);
mergeSort2(a);
print(a);
}
/**
* 遍历数组
* @param a
*/
public static <AnyType extends Comparable<? super AnyType>> void print(AnyType[] a){
for(int i=0;i<a.length;i++)
System.out.print(a[i]+"\t");
System.out.println("\n"+"----------------------------");
}
标签:
原文地址:http://www.cnblogs.com/kakaxisir/p/4324128.html