深入理解KMP算法

标签：kmp   字符串匹配   

一般在遇到字符串匹配的问题的时候，一种朴素的比较方式就是

int BFMatch(char *s,char *p)
{
    int i,j;
    i=0;
    while(i<strlen(s))
    {
        j=0;
        while(s[i]==p[j]&&j<strlen(p))
        {
            i++;
            j++;
        }
        if(j==strlen(p))
            return i-strlen(p);
        i=i-j+1;                //指针i回溯
    }
    return -1;    
}

S:  ababcababa

    P:  ababa

　 BF算法匹配的步骤如下

           i=0                                   i=1                             i=2                         i=3                          i=4

  第一趟:ababcababa         第二趟:ababcababa      第三趟:ababcababa    第四趟:ababcababa    第五趟:ababcababa

             ababa                            ababa                          ababa                        ababa                       ababa

            j=0                                   j=1                            j=2                         j=3                         j=4(i和j回溯)

              i=1                                 i=2                           i=3                            i=4                        i=3

 第六趟:ababcababa         第七趟:ababcababa       第八趟:ababcababa     第九趟:ababcababa    .....类似的方法一直进行下去

但是事实上在第5趟的过程中，不需要直接回溯到p数组的最开始，因为前面4个字符都是匹配的，j = 3的时候b是匹配的

P      a    b   a    b   a

j      0    1   2    3   4

next   -1   0   0    1   2

next[4] = 2  因此 j 应该回溯到元素2 的a，接着进行检测，一直循环，如果出现-1的情况，那么就是前面没有出现相同的部分了，那么从最开始进行检测

　即next[j]=k>0时，表示P[0...k-1]=P[j-k,j-1]

　因此KMP算法的思想就是：在匹配过程称，若发生不匹配的情况，如果next[j]>=0，则目标串的指针i不变，将模式串的指针j移动到next[j]的位置继续进行匹配；若next[j]=-1，则将i右移1位，并将j置0，继续进行比较。

Next按照递推的思想：

   根据定义next[0]=-1，假设next[j]=k, 即P[0...k-1]==P[j-k,j-1]

   1)若P[j]==P[k]，则有P[0..k]==P[j-k,j]，很显然，next[j+1]=next[j]+1=k+1;

   2)若P[j]!=P[k]，则可以把其看做模式匹配的问题，即匹配失败的时候，k值如何移动，显然k=next[k]。

　1.

　　首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

　　2.

　　因为B与A不匹配，搜索词再往后移。

　　3.

　　就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。

　　4.

　　接着比较字符串和搜索词的下一个字符，还是相同。

　　5.

　　直到字符串有一个字符，与搜索词对应的字符不相同为止。

　　6.

　　这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

　　7.

　　一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

　　8.

         A    B    C    D    A    B    D

j        0    1    2     3    4    5     6

next   -1  0    0    0     0     1    2

　　9.

这里匹配不上了，所以通过next数组找到对应的位置应该从j = 2的位置开始匹配

　　10.

　　因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

　　11.

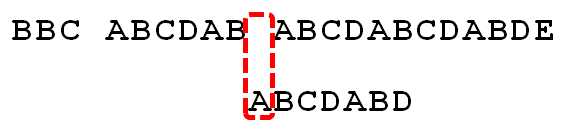
　　因为空格与A不匹配，从0位置开始匹配，那么只能从头开始了

　　12.

　　逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

　　13.

下面附上代码应该很好理解：

#include <iostream>
using namespace std;

//<算法中最重要的next特征矩阵，每一次匹配不成功的时候需要通过next
//<获取模式字符串跳转的位置
void GetNext(char *p,int * next) //<目前利用递归的方式进行赋值
	//<next[j] = k  表示p[0,k-1] = p[j-k,j-1]个元素
	//<如果p[k] = p[j] 那么next[j+1] = next[j]+1；
	//<如果p[k] != p[j] 那么类似模式匹配的过程,模式串为k，那么寻找合适的k  k= next[k]
{
	int k = -1; //<因为next[0] = -1
	int j = 0;
	next[0] = -1;
	while (j < (strlen(p)-1))//<因为后面有j++
	{
		if (k == -1 || p[k] == p[j]) //k == -1,是包括了已经匹配到最前面了，取值为0
		{
			k++;
			j++;
			next[j] = k; //<一般如果最后都没有匹配上，这里j++ = 0代表从头开始匹配
		}
		else
		{
			k = next[k]; //<因为当前没有匹配上，那么向前缩小前缀的长度，再匹配
		}
	}
}
int KMPmatch(char *p,char *s)
{
	int length = strlen(p);
	int *next = new int[length];
	GetNext(p,next);
	int i = 0; //<原始字符串
	int j = 0; //<模式字符串
	while (i < strlen(s))
	{
		if (j == -1 || (p[j] == s[i])) //<如果找到相应的元素，索引增加，同时如果j==-1，那么i++,j = 0；这里正好可以巧妙地放在一起进行
		{
			i++;
			j++;
		}
		else
		{
			j = next[j]; //<如果不匹配，根据next数组，进行跳转操作
		}
		if (j == strlen(p))
		{
			return i - j;
		}
	}
	delete next;
	return -1;

}
void main()
{
	char *s = "ababcababa";
	char *p = "ababa";
	int x = KMPmatch(p,s);
}

深入理解KMP算法

标签：kmp   字符串匹配   

原文地址：http://blog.csdn.net/xietingcandice/article/details/44181789