拓扑排序

一、概述

　　对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中全部顶点排成一个线性序列，使得图中随意一对顶点u和v，若<u，v> ∈E(G)，则u在线性序列中出如今v之前。
   　通常，这种线性序列称为满足拓扑次序(TopoiSicai Order)的序列，简称拓扑序列。
注意：
   　①若将图中顶点按拓扑次序排成一行，则图中全部的有向边均是从左指向右的。
   　②若图中存在有向环，则不可能使顶点满足拓扑次序。
   　③一个DAG的拓扑序列通常表示某种方案切实可行。
   　【例】一本书的作者将书本中的各章节学习作为顶点，各章节的先学后修关系作为边，构成一个有向图。按有向图的拓扑次序安排章节，才干保证读者在学习某章节时，其预备知识已在前面的章节里介绍过。
   　④一个DAG可能有多个拓扑序列。
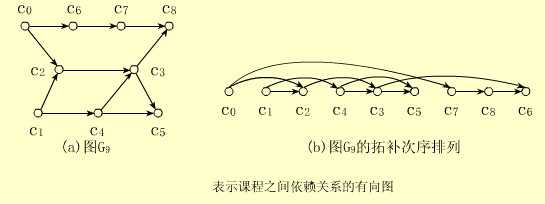
   　【例】对图G₉进行拓扑排序，至少可得到例如以下的两个(实际远不止两个)拓扑序列：C₀，C₁，C₂，C₄，C₃，C₅，C₇，C₈，C₆和C₀，C₇，C₉，C₁，C₄，C₂，C₃，C₆，C₅。
　　　　　　　　
　　⑤当有向图中存在有向环时，拓扑序列不存在　

二、无前趋的顶点优先的拓扑排序方法　　

　　该方法的每一步总是输出当前无前趋(即人度为零)的顶点，其抽象算法可描写叙述为：
    　　　　NonPreFirstTopSort(G){//优先输出无前趋的顶点
      　　　　  while(G中有入度为0的顶点)

do{
       　　　　　　从G中选择一个人度为0的顶点v且输出之；
     　　　　 　　 从G中删去v及其全部出边；
     　　　　        }
    　　　　    if(输出的顶点数目<|V(G)|)
     　　　　        //若此条件不成立，则表示全部顶点均已输出，排序成功。
       　　　　　　Error("G中存在有向环，排序失败！")；
    　　　　 }
注意：
    　无前趋的顶点优先的拓扑排序算法在详细存储结构下，为便于考察每一个顶点的人度，可保存各顶点当前的人度。为避免每次选入度为0的顶点时扫描整个存储空间，可设一个栈或队列暂存全部入度为零的顶点：
    　在開始排序前，扫描相应的存储空间，将人度为零的顶点均入栈(队)。以后每次选人度为零的顶点时，仅仅需做出栈(队)操作就可以。

三、无后继的顶点优先拓扑排序方法　　

1、思想方法
    　该方法的每一步均是输出当前无后继(即出度为0)的顶点。对于一个DAG，按此方法输出的序列是逆拓扑次序。因此设置一个栈(或向量)T来保存输出的顶点序列，就可以得到拓扑序列。若T是栈，则每当输出顶点时，仅仅需做入栈操作，排序完毕时将栈中顶点依次出栈就可以得拓扑序列。若T是向量，则将输出的顶点从T[n-1]開始依次从后往前存放，就可以保证T中存储的顶点是拓扑序列。
2、抽象算法描写叙述
　　算法的抽象描写叙述为：
    　　NonSuccFirstTopSort(G){//优先输出无后继的顶点
    　　  while(G中有出度为0的顶点)

do {
     　　           从G中选一出度为0的顶点v且输出v；
    　　           从G中删去v及v的全部人边
    　　        }
     　　   if(输出的顶点数目<|V(G)|)
     　　      Error("G中存在有向环，排序失败!")；
    　　  }
3、算法求精
    　在对该算法求精时，可用逆邻接表作为G的存储结构。设置一个向量outdegree[0..n-1]或在逆邻接表的顶点表结点中添加1个出度域来保存各顶点当前的出度；设置一个栈或队列来暂存全部出度为零的顶点。除了添加一个栈或向量T来保存输出的顶点序列外，该算法全然类似于NonPreFirstTopSort。

四、利用深度优先遍历对DAG拓扑排序　　

　　当从某顶点v出发的DFS搜索完毕时，v的全部后继必然均已被訪问过(想像它们均已被删除)，此时的v相当于是无后继的顶点，因此在DFS算法返回之前输出顶点v就可以得到 DAG的逆拓扑序列。

int map[Max][Max];  //採用邻接矩阵存储方式
int vis[Max],topo[Max];  //vis表示结点是否被訪问过
int m,n;  
bool Dfs(int u)  
{  
    vis[u]=-1;  //-1表示当前节点正在被訪问
    for(int v=1;v<=n;v++)  
    {  
        if(map[u][v])  
        {  
            if(vis[v]<0) {return false;}  //结点u的邻接点v若也正在被訪问，表示有环
            else if(!vis[v]&&!Dfs(v)) return false;//v未訪问，且遍历v失败，返回false  
        }  
    }  
    vis[u] = 1;topo[--t]=u;  
    return true;  
}  
bool toposort()  
{  
    t=n;  
    memset(vis,0,sizeof(vis));  
    for(int u=1;u<=n;u++)  
    {  
        if(!vis[u]){  
            if(!Dfs(u)) return false;  
        }  
    }  
    return true;  
} 

复杂度分析