关键路径(CriticalPath)算法

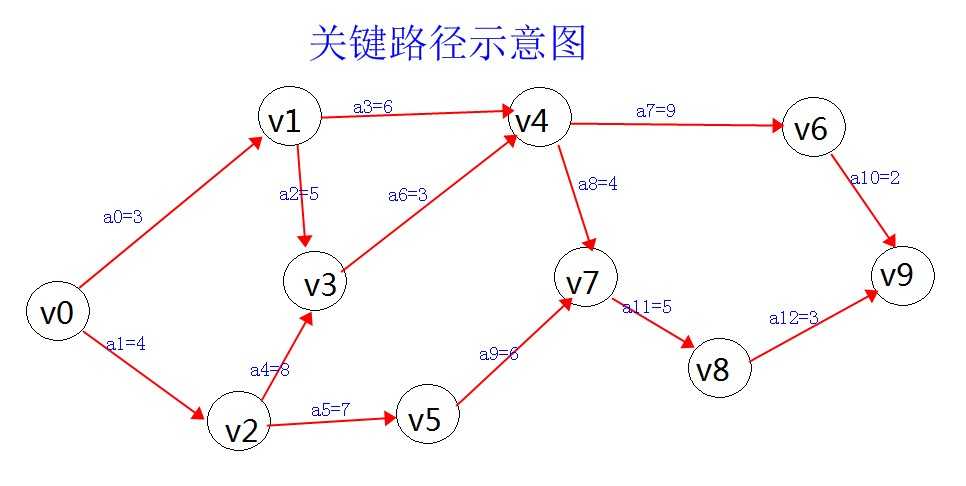
  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 #include <malloc.h>
  4 
  5 #define MAXVEX 30        //最大顶点数
  6 #define MAXEDGE 30        //最大边数
  7 #define INFINITY 65535    //∞
  8 
  9 //定义全局变量
 10 int *etv, *ltv;//事情最早发生和最迟发生指针数组
 11 int *stack2;//用于存储拓扑排序的栈
 12 int top2;//用于指向stack2栈指针
 13 
 14 /*    邻接矩阵结构    */
 15 typedef struct
 16 {
 17     int vexs[MAXVEX];//顶点下标
 18     int arc[MAXVEX][MAXVEX];//矩阵(路径)
 19     int numVertexes, numEdges;//当前图中的顶点数和边数
 20 }MGraph;
 21 
 22 
 23 /*    邻接表结构    */
 24 typedef struct EdgeNode    //
 25 {//边表结点
 26     int adjvex;//顶点下标
 27     int weight;//路径
 28     struct EdgeNode *next;//指向想一个边表结点
 29 }EdgeNode;
 30 
 31 typedef struct VertexNode
 32 {//顶点结点
 33     int in;//入度
 34     int data;//顶点信息
 35     EdgeNode *firstedge;//指向边表头指针
 36 }VertexNode, AdjList[MAXVEX];
 37 
 38 typedef struct
 39 {
 40     AdjList adjList;//顶点向量
 41     int numVertexes, numEdges;//顶点数和边数
 42 }graphAdjList, *GraphAdjList;
 43 
 44 
 45 
 46 void CreateMGraph(MGraph *G)
 47 {/*    构建图    */
 48     int i, j;
 49 
 50 //    printf("请输入顶点数和边数：\n");
 51     G->numVertexes = 10;
 52     G->numEdges = 13;
 53 
 54     //初始化顶点下标
 55     for(i=0; i<G->numVertexes; i++)
 56         G->vexs[i] = i;
 57 
 58     //初始化矩阵
 59     for(i=0; i<G->numVertexes; i++)
 60         for(j=0; j<G->numVertexes; j++)
 61             if(i == j)
 62                 G->arc[i][j] = 0;
 63             else
 64                 G->arc[i][j] = INFINITY;
 65 
 66     //内置输入
 67     G->arc[0][1] = 3;
 68     G->arc[0][2] = 4;
 69     G->arc[1][3] = 5;
 70     G->arc[1][4] = 6;
 71     G->arc[2][3] = 8;
 72     G->arc[2][5] = 7;
 73     G->arc[3][4] = 3;
 74     G->arc[4][6] = 9;
 75     G->arc[4][7] = 4;
 76     G->arc[5][7] = 6;
 77     G->arc[6][9] = 2;
 78     G->arc[7][8] = 5;
 79     G->arc[8][9] = 3;
 80 
 81     return ;
 82 }
 83 
 84 
 85 
 86 void CreateALGraph(MGraph G, GraphAdjList *GL)
 87 {/*    利用邻接矩阵，构建邻接表    */
 88     int i, j;
 89     EdgeNode *e;
 90     
 91     *GL = (GraphAdjList)malloc(sizeof(graphAdjList));//*GL代表主函数的GL指向
 92     (*GL)->numVertexes = G.numVertexes;/*    读取信息    */
 93     (*GL)->numEdges = G.numEdges;
 94 
 95     //初始化
 96     for(i=0; i<G.numVertexes; i++)
 97     {
 98         (*GL)->adjList[i].in = 0;
 99         (*GL)->adjList[i].data = G.vexs[i];//读取顶点下标
100         (*GL)->adjList[i].firstedge = NULL;
101     }
102 
103     //构建邻接表
104     for(i=0; i<G.numVertexes; i++)
105         for(j=0; j<G.numVertexes; j++)
106             if(0 != G.arc[i][j]  &&  INFINITY > G.arc[i][j])
107             {//若存在路径
108                 e = (EdgeNode *)malloc(sizeof(EdgeNode));//申请
109                 e->adjvex = j;//存顶点
110                 e->weight = G.arc[i][j];//存路径
111                 e->next = (*GL)->adjList[i].firstedge;//存表头指针
112                 (*GL)->adjList[i].firstedge = e;//头插
113                 (*GL)->adjList[j].in ++;//顶点入度+1
114             }
115     return ;
116 }
117 
118 
119 
120 void TopologicalSort(GraphAdjList GL)
121 {/*    拓扑排序    */
122     EdgeNode *e;
123     int i, gettop, k;
124     int top = 0;//用于指向stack栈顶
125     int count = 0;//技术输出
126     int *stack;//建栈存储入度位0的顶点
127     stack = (int *)malloc(sizeof(int));
128     for(i=0; i<GL->numVertexes; i++)//把所有入度位0的顶点如stack栈中
129         if(0 == GL->adjList[i].in)
130             stack[++top] = i;
131     
132     etv = (int *)malloc(sizeof(int) * GL->numVertexes);//最早发生etv指针申请空间
133     for(i=0; i<GL->numVertexes; i++)//初始化最早发生etv数组
134         etv[i] = 0;
135 
136     stack2 = (int *)malloc(sizeof(int) * GL->numVertexes);//存储拓扑排序序列
137     top2 = 0;//用于指向stack2栈顶
138     printf("Topological:\t");
139     while(0 != top)
140     {//若有顶点入度为0
141         gettop = stack[top--];//出栈
142         printf("%3d->", GL->adjList[gettop].data);//输出出栈的栈顶的顶点信息
143         count ++;//输出记数
144 
145         stack2[++top2] = gettop;//出栈元素赋给存储拓扑序列栈
146         
147         for(e=GL->adjList[gettop].firstedge; e; e=e->next)
148         {//出栈的栈顶元素若有邻接点
149             k = e->adjvex;//邻接点-顶点下标
150             if(! (--GL->adjList[k].in))//邻接点顶点下标-1(gettop已指向)，是否入度位0？
151                 stack[++top] = k;//是则入stack的栈
152 
153             /*出栈的最早发生时间值+出栈邻接表的路径  >  出栈邻接表顶点下标的最早发生时间值
154               就是v0-v1-v3和v0-v2-v3都是从起点到达汇点，3哪一个路径较远    */
155             if((etv[gettop] + e->weight) > etv[k])
156                 etv[k] = etv[gettop] + e->weight;
157         }
158     }
159     printf("\n");
160 
161     if(count < GL->numVertexes)//若有环，则结束程序
162         exit(-1);
163 
164     return ;
165 }
166 
167 
168 
169 void CriticalPath(GraphAdjList GL)
170 {/*    关键路径    */
171     EdgeNode *e;
172     int i, gettop, k, j;
173     int ete, lte;//最早发生和最迟发生的变量
174 
175     TopologicalSort(GL);//调用拓扑排序函数
176 
177     ltv = (int *)malloc(sizeof(int) * GL->numVertexes);//最迟发生指针边表指向申请空间
178     for(i=0; i<GL->numVertexes; i++)//初始化最迟发生数组
179         ltv[i] = etv[GL->numVertexes - 1];//起到汇最大值
180 
181     //输出最早发生数组
182     printf("etv:\t\t");
183     for(i=0; i<GL->numVertexes; i++)
184         printf("%3d->", etv[i]);
185     printf("\n");
186     
187     while(0 != top2)
188     {//存放拓扑排序数列
189         gettop = stack2[top2--];
190         for(e=GL->adjList[gettop].firstedge; e; e=e->next)
191         {
192             k = e->adjvex;
193             if((ltv[k] - e->weight) < ltv[gettop])
194                 ltv[gettop] = ltv[k] - e->weight;
195             /*最晚发生时间值(出stack2(存拓扑排序)栈元素的邻接点顶点下标) - 邻接路径   <    最晚发生数组【出栈元素0】
196               用拓扑排序的最长路径 - 邻接路径 < 最晚发生值[出栈元素]*/
197         }
198     }
199 
200     printf("ltv:\t\t");//输出最晚值数组
201     for(i=0; i<GL->numVertexes; i++)
202         printf("%3d->", ltv[i]);
203     printf("\n");
204 
205     for(j=0; j<GL->numVertexes; j++)
206         for(e=GL->adjList[j].firstedge; e; e=e->next)
207         {
208             k = e->adjvex;
209             ete = etv[j];//最早发生时间
210             lte = ltv[k] - e->weight;//最迟发生时间
211 
212             if(ete == lte)//相等即在关键路径上
213                 printf("<v%d - v%d> length : %d \n", GL->adjList[j].data, GL->adjList[k].data, e->weight);
214         }
215 
216     return ;
217 }
218 
219 int main(void)
220 
221 {    
222     MGraph G;
223     GraphAdjList GL;
224     system("title 关键路径");
225     CreateMGraph(&G);
226     CreateALGraph(G, &GL);
227     CriticalPath(GL);
228 
229     return 0;
230 }