标签:
查找算法
一、查找的基本概念
查找,也可称检索,是在大量的数据元素中找到某个特定的数据元素而进行的工作。查找是一种操作。
二、顺序查找
针对无序序列的一种最简单的查找方式。
时间复杂度为O(n)。
三、二分查找(折半查找)
针对已排序序列的一种查找方式。并且只适用于顺序存储结构的序列。要求序列中的元素基本不变,在需要做删除和插入操作的时候,会影响检索效率。
时间复杂度为O(logN)。
四、B树查找
B树又称二叉排序树(Binary Sort Tree)。
1、概念:
它或者是一棵空树;或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于左子树所在树的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于右子树所在树的根结点的值;
(3)左、右子树也分别为二叉排序树;
2、B树的查找:
时间复杂度与树的深度的有关。如果二叉树结构退化为链表,那么效率是O(n),如果二叉树结构接近于AVL树,那么其时间复杂度为O(logn)。
步骤:若根结点的关键字值等于查找的关键字,成功。
否则:若小于根结点的关键字值,递归查左子树。
若大于根结点的关键字值,递归查右子树。
若子树为空,查找不成功。
3、B树的插入:
首先执行查找算法,找出被插结点的父亲结点。
判断被插结点是其父亲结点的左儿子还是右儿子。将被插结点作为叶子结点插入。
若二叉树为空。则首先单独生成根结点。
注意:新插入的结点总是叶子结点,所以算法复杂度是O(h)。其中h指的是输的深度,如果是平衡二叉树,那么还可以是O(logn)。
定理:假设具有n个节点的树,所有树出现的可能性均等,那么树的平均深度为logn,所以查找、删除、插入的平均时间复杂度均为O(h) = O(logn)。
4、B树的删除:
如果删除的结点没有孩子,则删除后算法结束;
如果删除的结点只有一个孩子,则删除后该孩子取代被删除结点的位置;
如果删除的结点有两个孩子,则选择该结点的后继结点(该结点右孩子为根的树中的左子树中的值最小的点)作为新的根,同时在该后继结点开始,执行前两种删除算法,删除算法结束。
上面一句的意思是,如果被删除的节点有两个子节点,那么用该节点右子树中最小的节点来代替它,并按照上述删除方法删除那个最小的节点。
5、B树的一些深层次问题
5.1、B树删除节点问题,如果一棵树中有很多的节点,那么按照上述的方法,删除具有连个叶子结点的节点方法都是用右子树中最小的元素来替代,并删除掉这个最小的元素,这种方法会导致二叉树“失衡”,即二叉树向右倾斜,左侧的深度会远远大于右侧的深度,特别是经历了很多次的删除操作后,一种方法是交替的删除右子树中的最小节点和左子树中的最大节点,以防止树的失衡。这样的算法一般适用于大量的数据,在数据量小时起不到作用。
5.2 B树的查找、删除等操作的效率严重依赖于B树的结构,如何保证每次查找的时间复杂度为O(logn):一种方法是使用AVL树,每次进行插入删除操作后,都要使用算法调整树的结构,来保证树的叶子深度相差最大不超过1,这样就可以保证最坏的时间复杂度为O(logn)。这种方法的缺点是每次都要进行调整,其实际效率有待研究。近年来又有了一种新的方法,这种方法不再要求每次查找的最坏时间复杂度都是O(logn),而是可以保证在任意M次连续操作的最欢情况时间复杂度为O(M*logn)。这种树的结构叫做伸展树(splay tree)。
概念:AVL树,任何一个节点的左子树和右子树的高度最多差1。
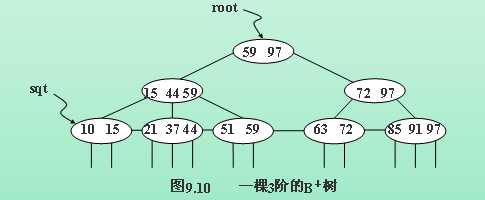
5、B+树
一棵m阶的B+树满足下列条件:
(1)每个结点最多m个孩子。
(2)除根结点和叶子结点外,其它每个结点至少有ém/2ù个孩子。
(3)根结点至少有两个孩子。
(4)所有的叶子结点在同一层,且包含了所有关键字信息。
(5)有k个孩子的分支结点包含k个关键字。
例如:
五、散列(hash)表
关键字:哈希函数、装填因子、冲突、同义词;
关键字和和存储的地址建立一个对应的关系:
Add = Hash(key);
解决冲突方法:
开放定址法 – 探测方式:线性探测、二次探测。
分离链接法 – 利用链表的方式。
查找找效率不依赖于数据长度n,查找效率非常快,很多能达到O(1),查找的效率是a(装填因子)的函数,而不是n的函数。因此不管n多大都可以找到一个合适的装填因子以便将平均查找长度限定在一个范围内。
概念:
装填因子:hash表中关键字的个数/hash表长 n/m。装填因子一般选择0.5左右。
标签:
原文地址:http://www.cnblogs.com/wll-zju/p/4333756.html