标签:
1.二叉排序树的定义
二叉排序树(Binary Sorting Tree)的定义如下:
二叉树或者是一棵空树,或者是一棵具有以下性质的二叉树:
(1)若它有左子树,则左子树上所有结点的数据均小于根结点的数据。
(2)若它有右子树,则右子树上所有结点的数据均大于根结点的数据。
(3)左、右子树本身又各是一棵二叉排序树。
2.插入结点
向二叉排序树中插入一个结点,使此树仍为二叉排序树。假设以t为树根指针,再向该二叉树中增加新的关键字key。具体过程如下:
(1)申请保存结点p的内存,将关键字保存在结点的数据域。
(2)在二叉排序树中查找插入结点p的父结点。
(3)比较p 结点的数据与父结点的数据,决定将p插入到父结点的左子树还是右子树。
3.查找结点
根据二叉排序树的定义,在二叉排序树t中查找指定关键字key的过程如下:
(1)从根结点开始查找。
(2)若结点为空,查找失败。
(3)若key值与结点的数据相等,表示查找成功,返回结点指针。
(4)若key值小于结点的数据,继续在当前结点的左子树查找。
(5)若key值大于结点的数据,继续在当前结点的右子树查找。
4.删除结点
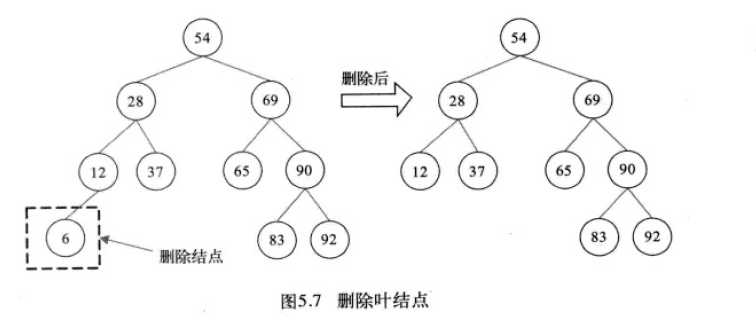
(1)若删除结点是二叉排序树的叶结点,即t->left和t->right都为空。这时,由于删除该结点不会破坏二叉排序树的结构,只需修改t结点的父结点的指针,并释放t结点占用的内存即可。
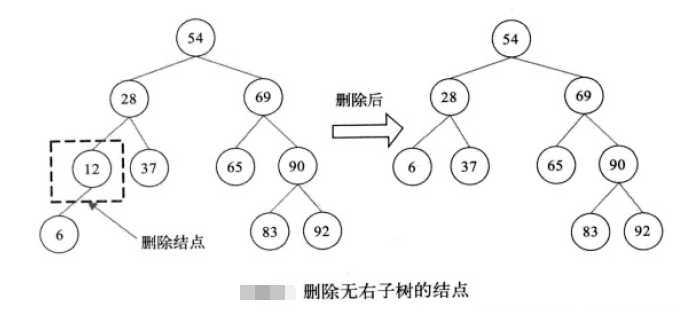
(2)若t结点只有一个子树(即t->left或t->right有一个为空),这时,只需要修改t结点的父结点,使其子结点指针的值为t->left或t->right即可。
(3)若t结点有两个子树(即t->left和t->right都不为空),此时的操作相对要复杂些,需从二叉排序树的中序遍历中找出被删除结点的后继结点。
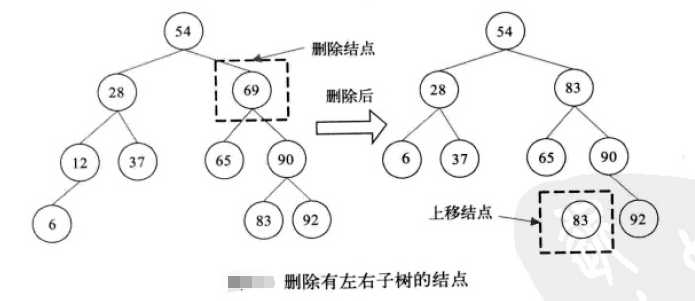
要找出被删除结点的中序遍历后继结点,该后继结点的值应该比被删除结点大,那么该结点就应该位于被删除结点的右子树。同时,被删除结点的后继结点又应该比后续其他结点的值都要小,因此,该结点应该是被删除结点右子树中的最小值。根据二叉排序树的特点,最小值应该是位于右子树的最左侧的叶结点。
因此,只需在被删除结点的右子树中查找,找到最左侧的叶结点,将该叶结点的值移到被删除结点即可。
1 //----------二叉排序树的创建,查找与删除,以下代码是其所有左子树的结点均小于根的值,其右子树的值均小于其根的值。----------- 2 #include<stdio.h> 3 #include<malloc.h> 4 typedef int datatype; 5 #define ENDKEY 0 6 typedef struct BSTree 7 { 8 datatype data; 9 struct BSTree *lchild; 10 struct BSTree *rchild; 11 }BSTreenode,*BSTree; 12 typedef struct node 13 { 14 BSTree BST; 15 16 struct node *next; 17 }QueueNode; 18 typedef struct Queue 19 { 20 QueueNode *front; 21 QueueNode *tail; 22 }Queue; 23 void InitQueue(Queue *Q) 24 { 25 Q->front=(QueueNode *)malloc(sizeof(QueueNode)); 26 if(Q->front)/*初始化为一个空的队列*/ 27 { 28 Q->tail=Q->front; 29 Q->front->next=NULL; 30 31 } 32 } 33 void EnterQueue(Queue *Q,BSTree p) 34 { 35 QueueNode *newnode; 36 newnode=(QueueNode *)malloc(sizeof(QueueNode)); 37 if(newnode) 38 { 39 newnode->BST=p; 40 newnode->next=NULL; 41 Q->tail->next=newnode; 42 Q->tail=newnode; 43 44 } 45 } 46 void DeQueue(Queue *Q,BSTree *p) 47 { 48 QueueNode *q; 49 if(Q->front==Q->tail) 50 return ; 51 q=Q->front->next; 52 Q->front->next=q->next; 53 if(Q->tail==q) 54 Q->tail=Q->front; 55 *p=q->BST; 56 free(q); 57 } 58 int Empty(Queue Q) 59 { 60 if(Q.front==Q.tail) 61 return 1; 62 return 0; 63 } 64 void Output(BSTree BT)//利用队列层析显示二叉排序树的初始状态元素 65 { 66 Queue Q; 67 68 BSTree p,q; 69 InitQueue(&Q); 70 q=p=BT; 71 if(p) 72 EnterQueue(&Q,p); 73 while(!Empty(Q)) 74 { 75 DeQueue(&Q,&q); 76 printf("%3d",q->data); 77 if(q->lchild) 78 EnterQueue(&Q,q->lchild); 79 if(q->rchild) 80 EnterQueue(&Q,q->rchild); 81 } 82 83 } 84 void InsertBT(BSTree *BT,datatype key)//插入方式建立二叉树 85 { 86 BSTreenode *bst; 87 if((*BT)==NULL) 88 { 89 bst=(BSTreenode *)malloc(sizeof(BSTreenode)); 90 bst->data=key; 91 bst->lchild=NULL; 92 bst->rchild=NULL; 93 *BT=bst; 94 } 95 else if(key<(*BT)->data)//小于根的元素放到左子树 96 { 97 InsertBT(&((*BT)->lchild),key); 98 } 99 else if(key>(*BT)->data)//大于根的元素放到右子树 100 { 101 InsertBT(&((*BT)->rchild),key); 102 } 103 104 105 } 106 void Create_BSTree(BSTree *BT) 107 { 108 datatype key; 109 (*BT)=NULL; 110 printf("Input the key (input 0 to end the input ):"); 111 scanf("%d",&key); 112 while(key!=ENDKEY) 113 { 114 InsertBT(BT,key); 115 scanf("%d",&key); 116 } 117 } 118 void InorderOutput(BSTree *BT)//利用中序遍历输出二叉树的元素 119 { 120 if(*BT) 121 { 122 InorderOutput(&((*BT)->lchild)); 123 printf("%3d",(*BT)->data); 124 InorderOutput(&((*BT)->rchild)); 125 } 126 } 127 BSTree FindBT(BSTree BT,int key) 128 { 129 BSTree p; 130 p=BT; 131 while(p) 132 { 133 if(p->data==key) return p; 134 else if(key<p->data) p=p->lchild; 135 else p=p->rchild; 136 } 137 return NULL; 138 } 139 BSTree DeleteKey(BSTree BT,int key) 140 { 141 BSTree f,p,s,q; 142 p=BT; 143 f=NULL; 144 while(p) 145 { 146 if(p->data==key) break; 147 148 f=p; 149 if(p->data<key) p=p->rchild; 150 else 151 p=p->lchild; 152 } 153 if(p==NULL) 154 printf("Cannot find the data\n"); 155 if(p->lchild==NULL&&p->rchild==NULL)//如果p是叶子节点 156 { 157 if(f) 158 { 159 if(f->lchild==p) 160 f->lchild=NULL; 161 else 162 f->rchild=NULL; 163 } 164 free(p); 165 printf("the data has been deleted\n"); 166 return BT; 167 } 168 if(p->lchild==NULL)//要找的结点没有左子树 169 { 170 if(f==NULL) 171 BT=p->rchild; 172 else if(f->lchild==p) 173 f->lchild=p->lchild; 174 else 175 f->rchild=p->rchild; 176 free(p); 177 } 178 else//要找的结点有左子树 179 { 180 q=p; 181 s=p->lchild; 182 while(s->rchild) 183 { 184 q=s; 185 s=s->rchild; 186 } 187 if(p==q) q->lchild=s->lchild; 188 else 189 q->rchild=s->lchild; 190 p->data=s->data; 191 free(s); 192 193 } 194 return BT; 195 196 197 } 198 void main() 199 { 200 BSTreenode *BT,*find,*BST; 201 int key; 202 int Delete_key; 203 Create_BSTree(&BT);//创建一颗二叉树 204 Output(BT); 205 printf("\nafter Inorder the tree as follow :\n"); 206 InorderOutput(&BT);//中序遍历可以把二叉树按递增的顺序输出 207 printf("\nInput the data you wan to find :"); 208 scanf("%d",&key); 209 find=FindBT(BT,key); 210 if(find) 211 212 printf("find the data %d\n",find->data); 213 else 214 printf("cannot find the data\n"); 215 printf("Input the data you want to delete: "); 216 scanf("%d",&Delete_key); 217 BST=DeleteKey(BT,Delete_key); 218 InorderOutput(&BST);//删除后再次显示二叉树序列 219 printf("\n"); 220 }
1 //二叉排序树操作类: 2 /** 3 * 二叉排序树 4 * 定义:左子树若不为空,左子树均小于根节点;若右子树不为空,右子树均大于根节点。左右子树分别为二叉排序树。 5 * 特点: 6 * 复杂度为:O(logn) 7 * 最坏情况:O(n) 8 * 由此引申出来的概念:平衡二叉树、红黑树 9 * 10 * @author CheN 11 * 12 */ 13 public class BinarySortingTree { 14 /** 15 * 将数组转化为二叉排序树 16 * @param array 17 */ 18 public static void buildBinarySortingTree( int[] array ){ 19 BinaryTreeNode root = new BinaryTreeNode(); 20 root.setValue(array[0]); 21 for( int i = 1 ; i < array.length ; i++ ){ 22 addBinarySortingTreeNode( root , array[i] ); 23 } 24 } 25 26 /** 27 * 将二叉树转化为二叉排序树简单二叉排序树 28 * @param root 29 */ 30 public static void buildBinarySortingTree( BinaryTreeNode root ){ 31 List<BinaryTreeNode> list = root.toList(); 32 for(int i = 0 ; i < list.size() ; i++ ){ 33 if( list.get(i) == root ) 34 continue; 35 addBinarySortingTreeNode( root , list.get(i).getValue() ); 36 } 37 } 38 39 /** 40 * 将数组转化为二叉排序树,注:array中不要包含root已赋值给root的值,否则会多出一个值 41 * @param root 42 * @param array 43 */ 44 public static void buildBinarySortingTree( BinaryTreeNode root , int[] array ){ 45 for(int i = 0 ; i < array.length ; i++ ){ 46 addBinarySortingTreeNode( root , array[i] ); 47 } 48 } 49 50 /** 51 * 将二叉树转化为二叉排序树简单二叉排序树:newRoot须为原树中的某一结点 52 * @param root 53 * @param newRoot 54 */ 55 public static void buildBinarySortingTree( BinaryTreeNode root , BinaryTreeNode newRoot ){ 56 List<BinaryTreeNode> list = root.toList(); 57 for(int i = 0 ; i < list.size() ; i++ ){ 58 if( list.get(i) == newRoot ) 59 continue; 60 addBinarySortingTreeNode( newRoot , list.get(i).getValue() ); 61 } 62 } 63 64 /** 65 * 将指定的元素插入二叉排序树中 66 * @param root 67 * @param target 68 */ 69 private static void addBinarySortingTreeNode( BinaryTreeNode root , int target ){ 70 int value = root.getValue(); 71 if( target < value ){//插入右子树 72 if(root.getLeftChild()==null){ 73 BinaryTreeNode node=new BinaryTreeNode(target); 74 root.setLeftChild(node); 75 }else{ 76 addBinarySortingTreeNode( root.getLeftChild() , target ); 77 } 78 }else if(target>value){ 79 if(root.getRightChild()==null){ 80 BinaryTreeNode node=new BinaryTreeNode(target); 81 root.setRightChild(node); 82 }else{ 83 addBinarySortingTreeNode( root.getRightChild() , target ); 84 } 85 } 86 } 87 88 /** 89 * 查找二叉排序树 90 * @param root 91 * @param target 92 */ 93 public static BinaryTreeNode BinarySerch( BinaryTreeNode root,int target ){ 94 if( root == null ){ 95 return null; 96 }else if(root.getValue()==target){ 97 return root; 98 }else if(root.getValue()>target){ 99 return BinarySerch(root.getLeftChild(),target); 100 }else{ 101 return BinarySerch(root.getRightChild(),target); 102 } 103 } 104 105 /** 106 * 获取二叉排序树最小值(即最左侧结点) 107 * @param root 108 * @return 109 */ 110 public static BinaryTreeNode getMinFromBinarySortingTree( BinaryTreeNode root ){ 111 if( root.getLeftChild() == null ){ 112 return root; 113 }else{ 114 return getMinFromBinarySortingTree( root.getLeftChild() ); 115 } 116 } 117 118 /** 119 * 获取二叉排序树最大值(即最右侧结点) 120 * @param root 121 * @return 122 */ 123 public static BinaryTreeNode getMaxFromBinarySortingTree( BinaryTreeNode root ){ 124 if( root.getRightChild() == null ){ 125 return root; 126 }else{ 127 return getMaxFromBinarySortingTree( root.getRightChild() ); 128 } 129 } 130 131 /** 132 * 在二叉排序树上增加结点 133 * @param root 134 * @param node 135 * @return 136 */ 137 public static boolean addNodeToBinarySortingTree( BinaryTreeNode root , BinaryTreeNode node ){ 138 if( root.getValue() > node.getValue() ){ 139 if( root.getLeftChild() == null ){ 140 BinaryTree3Links.addLeftChild(root, node); 141 return true; 142 } 143 return addNodeToBinarySortingTree( root.getLeftChild() , node ); 144 }else{ 145 if( root.getRightChild() == null ){ 146 BinaryTree3Links.addRightChild(root, node); 147 return true; 148 } 149 return addNodeToBinarySortingTree( root.getRightChild() , node ); 150 } 151 } 152 153 /** 154 * 在二叉排序树上删除节点 155 * @param node 156 * @return 157 */ 158 public static boolean deleteNodeFromBinarySortingTree( BinaryTreeNode node ){ 159 BinaryTreeNode parent = node.getParent(); 160 BinaryTreeNode rightChild = node.getRightChild(); 161 BinaryTreeNode leftChild = node.getLeftChild(); 162 if( BinaryTree3Links.isLeaf(node) ){//如果是叶子结点,则直接删了 163 if( BinaryTree3Links.isLeftChild(node)) 164 parent.setLeftChild(null); 165 else 166 parent.setRightChild(null); 167 node.setParent(null); 168 return true; 169 }else{ 170 if( leftChild == null ){//如果只有右结点,则将右结点与父结点相连 171 if( BinaryTree3Links.isLeftChild(node)){ 172 parent.setLeftChild(rightChild); 173 }else{ 174 parent.setLeftChild(leftChild); 175 } 176 rightChild.setParent(parent); 177 node.setRightChild(null); 178 node.setParent(null); 179 return true; 180 }else if(rightChild == null ){//如果只有左结点,则将左结点与父结点相连 181 if( BinaryTree3Links.isLeftChild(node)){ 182 parent.setRightChild(rightChild); 183 }else{ 184 parent.setRightChild(leftChild); 185 } 186 leftChild.setParent(parent); 187 node.setLeftChild(null); 188 node.setParent(null); 189 return true; 190 }else{//若左右子树都存在,则在左子树中找到最大的一个结点替代这个结点,若该节点有左子树,则将其左子树与其父结点连接 191 BinaryTreeNode temp = leftChild; 192 while( temp.getRightChild() != null ){ 193 temp = temp.getRightChild(); 194 } 195 if( temp.getLeftChild() != null ){ 196 BinaryTreeNode tempParent = temp.getParent(); 197 temp.getLeftChild().setParent(tempParent); 198 tempParent.setRightChild(temp.getLeftChild()); 199 } 200 temp.setParent(parent); 201 temp.setLeftChild(leftChild); 202 temp.setRightChild(rightChild); 203 node.setParent(null); 204 node.setLeftChild(null); 205 node.setRightChild(null); 206 } 207 } 208 return false; 209 } 210 }
标签:
原文地址:http://www.cnblogs.com/wxb713/p/4341399.html