标签:
1、动态规划解决过程
1)描述一个最长公共子序列
如果序列比较短,可以采用蛮力法枚举出X的所有子序列,然后检查是否是Y的子序列,并记录所发现的最长子序列。如果序列比较长,这种方法需要指数级时间,不切实际。
LCS的最优子结构定理:设X={x1,x2,……,xm}和Y={y1,y2,……,yn}为两个序列,并设Z={z1、z2、……,zk}为X和Y的任意一个LCS,则:
(1)如果xm=yn,那么zk=xm=yn,而且Zk-1是Xm-1和Yn-1的一个LCS。
(2)如果xm≠yn,那么zk≠xm蕴含Z是是Xm-1和Yn的一个LCS。
(3)如果xm≠yn,那么zk≠yn蕴含Z是是Xm和Yn-1的一个LCS。
定理说明两个序列的一个LCS也包含两个序列的前缀的一个LCS,即LCS问题具有最优子结构性质。
2)一个递归解
根据LCS的子结构可知,要找序列X和Y的LCS,根据xm与yn是否相等进行判断的,如果xm=yn则产生一个子问题,否则产生两个子问题。设C[i,j]为序列Xi和Yj的一个LCS的长度。如果i=0或者j=0,即一个序列的长度为0,则LCS的长度为0。LCS问题的最优子结构的递归式如下所示:
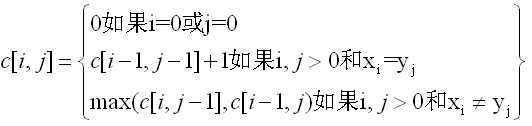
实现算法:
void lcs_length() { int i,j; for(i=1;i<=X_LEN;i++) c[i][0]=0; for(i=0;i<=Y_LEN;i++) c[0][i]=0; for(i=1;i<=X_LEN;i++) for(j=1;j<=Y_LEN;j++) { if(s1[i-1]==s2[j-1]) { c[i][j]=c[i-1][j-1]+1; b[i][j]=‘\\‘; } else if(c[i-1][j]>=c[i][j-1]) { c[i][j]=c[i-1][j]; b[i][j]=‘|‘; } else { c[i][j]=c[i][j-1]; b[i][j]=‘-‘; } } }
动态规划有一个经典问题是最长公共子序列,但是这里的子序列不要求连续,如果要求序列是连续的,我们叫公共子串,那应该如何得到这个串呢?
最简单的方法就是依次比较,以某个串为母串,然后生成另一个串的所有长度的子串,依次去母串中比较查找,这里可以采用先从最长的子串开始,减少比较次数,但是复杂度依然很高!
然后重新看一下这个问题,我们建立一个比较矩阵来比较两个字符串str1和str2
定义 lcs(i,j) ,当str1[i] = str2[j]时lcs(i,j)=1,否则等于0。
example:
str1 = "bab"
str2 = "caba"
建立矩阵
--b a b
c 0 0 0
a 0 1 0
b 1 0 1
a 0 1 0
连续i子串的特点就是如果str1[i]和str2[j]是属于某公共子串的最后一个字符,那么一定有str1[i]=str2[j] && str1[i-1] = str2[j-1],从矩阵中直观的看,就是由“1”构成的“斜线”代表的序列都是公共子串,那么最长公共子串肯定就是斜线“1”最长的那个串。
那么现在问题就可以转化了,只要构造出如上的一个矩阵,用n^2的时间就可以得到矩阵,然后再到矩阵中去寻找最长的那个“1”构成的斜线就可以了!那么,现在又有了新的问题?如何快速的找到那个“1”构成的最长斜线呢?
采用DP的思想,如果str1[i] = str2[j],那么此处的包含str1[i] 和 str2[j]公共子串的长度必然是包含str1[i-1]和str2[j-1]的公共子串的长度加1,那么现在我们可以重新定义lcs(i,j),即是lcs(i,j) = lcs(i-1,j-1) + 1,反之,lcs(i,j) = 0。那么上面的矩阵就变成了如下的样子:
--b a b
c 0 0 0
a 0 1 0
b 1 0 2
a 0 2 0
现在问题又变简单了,只需要花n^2的时间构造这样一个矩阵,再花n^2的时间去找到矩阵中最大的那个值,对应的就是最长公共子串的长度,而最大值对应的位置对应的字符,就是最长公共子串的最末字符。
算法还可以改进,我们可以将查找最大长度和对应字符的工作放在构造矩阵的过程中完成,一边构造一边记录当前的最大长度和对应位置,这样就节省了n^2的查找时间。
实现算法:
/* 最长公共子串 DP */ int dp[30][30]; void LCS_dp(char * X, int xlen, char * Y, int ylen) { maxlen = maxindex = 0; for(int i = 0; i < xlen; ++i) { for(int j = 0; j < ylen; ++j) { if(X[i] == Y[j]) { if(i && j) //i和j都不为0的时候 { dp[i][j] = dp[i-1][j-1] + 1; } if(i == 0 || j == 0) { dp[i][j] = 1; } if(dp[i][j] > maxlen) { maxlen = dp[i][j]; //最长的子串长度 maxindex = i + 1 - maxlen;//求出公共子串开始的位置 } } } } outputLCS(X); }
从第二个字符开始逐个加入不重复子串中,如果当前与已有的不重复字符串中字符存在重复的,则此字符不能加入,此时,需要计算最大不重复的长度,然后将不重复串的第一个下标更新为重复字符的下一个。
int lengthOfLongestSubstring(string s) { if(s.empty()) return 0; int maxLen=1; int i,j,k; j=0; k=0; for(i=1; i<(int)s.size(); i++) { j=k; while(j<i) { if(s[i]!=s[j]) j++; else { if(i-k>maxLen) maxLen=i-k; k=j+1; break; } } } if(i-k>maxLen) maxLen=i-k; return maxLen; }
此可以使用动态规划实现,leetcode上的题目。
string longestPalindrome(string s) { if(s.empty()) return NULL; int start=0; int end=0; int n=s.length(); bool dp[n][n]; memset(dp,false,sizeof(dp)); int i; dp[0][0]=true; for(i=1;i<n;i++) { dp[i][i]=true; dp[i][i-1]=true; } int k;//k用于记录从i开始的子串的长度,当长度为1是肯定是回文,从len=2开始判断 for(k=2;k<=n;k++) { for(i=0;i<=n-k;i++) { if(s[i]==s[i+k-1]&&dp[i+1][i+k-2]) { dp[i][i+k-1]=true; if(k>end-start+1) { start=i; end=i+k-1; } } } } return s.substr(start,end-start+1); }
方法一:DP
像LCS一样,从后向前分析,很容易想到,第i个元素之前的最长递增子序列的长度要么是1(单独成一个序列),要么就是第i-1个元素之前的最长递增子序列加1,可以有状态方程:
LIS[i] = max{1,LIS[k]+1},其中,对于任意的k<=i-1,arr[i] > arr[k],这样arr[i]才能在arr[k]的基础上构成一个新的递增子序列。
int LIS(int arr[],int n) { int *dp=new int[n]; for(int i=0;i<n;i++) { dp[i]=1; for(int j=0;j<i;j++) { if(arr[i]>arr[j]&&dp[i]<dp[j]+1) dp[i]=dp[j]+1; }
} }
可能有两种情况,一种是如果和全是负数的时候是返回0还是数组中的最小的一个负数呢?在于数组的元素是不是必须选或者不选。可以看看http://blog.csdn.net/v_july_v/article/details/6444021
如果数组中的元素非要选择,实现代码:
int maxSubArray(int A[], int n) { if(n==0) return 0; int maxSum=A[0]; int sum=A[0]; int i; for(i=1;i<n;i++) { if(sum<0) sum=A[i]; else sum+=A[i]; if(maxSum<sum) { maxSum=sum; } } return maxSum; }
否则,可以令sum和maxSum=0.
最长公共子序列|最长公共子串|最长重复子串|最长不重复子串|最长回文子串|最长递增子序列|最大子数组和
标签:
原文地址:http://www.cnblogs.com/wuchanming/p/4348971.html