标签:
画外音:没想做到15-2题也是费了一番周折,看来《算法导论》里题都不是白给的
整齐打印问题: 考虑在一个打印机上整齐地打印一段文章的问题。输入的正文是n个长度分别为L1、L2、……、Ln(以字符个数度量)的单词构成的序列。我们希望将这个段落在一些行上整齐地打印出来,每行至多M个字符。“整齐度”的标准如下:如果某一行包含从i到j的单词(i<j),且单词之间只留一个空格,则在行末多余的空格字符个数为 M - (j-i) - (Li+ …… + Lj),它必须是非负值才能让该行容纳这些单词。我们希望所有行(除最后一行)的行末多余空格字符个数的立方和最小。请给出一个动态规划的算法,来在打印机整齐地打印一段又n个单词的文章。分析所给算法的执行时间和空间需求。
在网上非常认真地看了几篇关于这个整齐打印的博客,发现真的都是错误的!非常坑人!传送门我就不开了,虽说对思路会一些启发但是少一个准确的版本来解决这个问题。
这个问题的核心思想依然是动态规划,而动态规划的关键在于找到整个解决过程的最优子结构。
我们声明一个数组来储存随着单词长度增加的动态最优解op[](在下面的代码中为了实现随机长度解决该问题使用了vector动态分配),在动态规划的过程之中的第n级最优子结构我们需要计算的是 1)第n-1到1级的最优化解 2)连续串接的 i 到 j 个单词在limit长度限制下的代价(weight)。
公式表达为 op[n]=min{op[k-1]+cost(k,n)...} ////k为循环遍历的值 k从n到 1,整个计算过程为状态转移的过程
/*当 k==n的时候,表示前面n-1个单词构成的最优化结构不需要对齐,直接以新的一行添加入 */
为了尽量减少算法的时间复杂度,我们可以使k从n向小遍历,这样以来可以检测当前 从k到n个单词所需要的代价大于一行的限制的时候跳出循环。
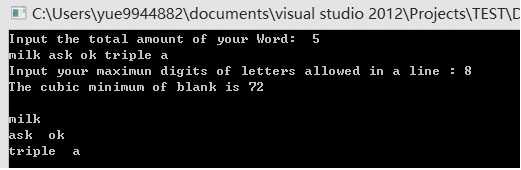
多次运行测试没有发现问题,欢迎帮我找一些BUG
#include<string>
#include<iostream>
#include<vector>
#include<cstdlib>
#define MAX_VAL 999999
using namespace std;
int g_iLast=0;
int g_iLimit=MAX_VAL;
int g_iLen=0;
vector<int> g_vecOp; ////optimal amount for weight
vector<string> g_vecWord; ////////Storing the words
vector<int> g_vecIndex;
int space(int index){
////////// index>=1
int total=g_iLimit;
for(int i=1;i<=g_iLen;i++){
if(g_vecIndex[i]==index){
total-=g_vecWord[i-1].size();
total--;
}
}
return total;////// A bug!
}
int space(int i,int j){
/////// 1<=i<=j<=len
int total=0;
for(int x=i;x<=j;x++){
total+=g_vecWord[x-1].size();
}
return g_iLimit-j+i-total;
}
void optimal(){
int iCur=1;
for(int i=1;i<=g_iLen;i++){
////// Descend Order to Save More Time
g_vecOp[i]=MAX_VAL;
int iSpace=space(iCur);
int iSize=g_vecWord[i-1].size();
if(iSpace>=iSize){
//////// The Space Enough to append
g_vecIndex[i]=iCur;
g_vecOp[i]=g_iLast+(iSpace-iSize)*(iSpace-iSize)*(iSpace-iSize);
}else{
/////// If Not
iCur++;
g_iLast=g_vecOp[i-1];
int min=MAX_VAL;
for(int j=i;j>1;j--){
int s=space(j,i);
if(s<0)break;
int temp=g_vecOp[j-1]+s*s*s;
if(min>temp){
min=temp;
for(int m=j;m<=i;m++){
g_vecIndex[m]=iCur;
}
}
}g_vecOp[i]=min;
g_vecIndex[i]=iCur;
}
}
cout<<"The cubic minimum of blank is "<<g_vecOp[g_iLen]<<endl<<endl;
}
int main(){
cout<<"Input the total amount of your Word: "<<ends;
cin>>g_iLen;
///////////////////////
string szTmp;
for(int i=0;i<g_iLen;i++){
cin>>szTmp;
g_vecWord.push_back(szTmp);
}
///////////////////////
cout<<"Input your maximun digits of letters allowed in a line :"<<ends;
cin>>g_iLimit;
for(int i=0;i<=g_iLen;i++){
g_vecOp.push_back(0);
g_vecIndex.push_back(0);
}
/////////////////////// Initializing Complete
optimal();
//////////////////////Outputting
int now=1;
for(int i=1;i<=g_iLen;i++){
if(g_vecIndex[i]>now){
now++;
cout<<endl<<g_vecWord[i-1]<<‘ ‘<<ends;
}else{
cout<<g_vecWord[i-1]<<‘ ‘<<ends;
}
}
return 0;
}
标签:
原文地址:http://www.cnblogs.com/guguli/p/4348736.html