标签:
Implement int sqrt(int x).
这道题本质上是求sqrt(x)下最大的整数。二分查找是比较容易想到的方法。另,在网上又学习了下别人的牛顿迭代法。
这是我原来的写法,写入是错误的,复杂度太高
class Solution { public: int sqrt(int x) { if (x <= 0) return 0; if (x == 0 || x == 1) return x; long long start = 1; long long end = x >> 1; int index = start; while (start <= end) { index = (start + end) >> 1; if (index*index == x) return index; else{ if (end*end <= x) return end; if (end - start == 1) return start; if (index*index > x) end = index - 1; if (index*index < x) start = index ; } } return index; } };
其实二分查找的思想是对的,只不过在某些小细节上海需要尤为注意一下。
标准代码可以这么写:
class Solution { public: int sqrt(int x) { long long i = 0; long long j = x / 2 + 1; while (i <= j) { long long mid = (i + j) / 2; long long sq = mid * mid; if (sq == x) return mid; else if (sq < x) i = mid + 1; else j = mid - 1; } return j; } };
完美的考虑了溢出的问题。这是我应该好好学习的地方。
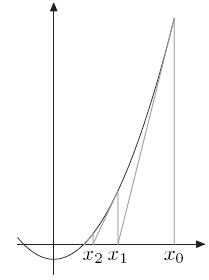
有此方法,可得到迭代公式xi+1=xi - (xi2 - n) / (2xi) = xi - xi / 2 + n / (2xi) = xi / 2 + n / 2xi = (xi + n/xi) / 2。
于是有如下代码:
int sqrt(int x) { if (x == 0) return 0; double last = 0; double res = 1; while (res != last) { last = res; res = (res + x / res) / 2; } return int(res); }
求解double的题目,可参考如上代码
double sqrt(double x) { if (x == 0) return 0; double last = 0.0; double res = 1.0; while (!euqal(res,last)) { last = res; res = (res + x / res) / 2; } return res; } bool euqal(double num1, double num2) { if ((num1 - num2) < 0.0000001 && (num1 - num2) > -0.0000001) return true; else return false; }
参考:
http://www.cnblogs.com/AnnieKim/archive/2013/04/18/3028607.html
标签:
原文地址:http://www.cnblogs.com/chengxuyuanxiaowang/p/4349933.html