《算法导论》学习笔记一：课程简介及算法分析

标签：

MIT的算法导论公开课，很多年前就看到了，一直没有坚持去看，最近找暑假实习，面试基本都是算法，只好抽时间去狂刷leetcode，也借着这个机会希望把这个视频看完，把算法的基本功打扎实，这个公开课讲得还是挺不错的。

之前学习其他东西的时候，记了很多笔记，最后都丢了，想再翻看的时候已经找不到，于是想到把学习笔记放到博客上，这样方便以后自己查询。

公开课视频地址：http://open.163.com/special/opencourse/algorithms.html

第一节：课程简介及算法分析

第一集视频一半的时间都是给学生讲课程要求和作业情况的，剩下的才讲了点干货，以Insertion Sort和Merge Sort为切入点，讲解算法分析。

Insertion Sort:

Pseudocode

Insertion (A, n) // Sorts A[1, ... , n]
for j ← 2 to n
    do key ← A[j]
        i ← j - 1
        while i > 0 and A[i] > key
            do A[i+1] ← A[i]
            i ← i - 1
        A[i+1] ← key

Example:

8 2 4 9 3 6

2 8 4 9 3 6

2 4 8 9 3 6

2 4 8 9 3 6

2 3 4 8 9 6

2 3 4 6 8 9

Running Time:

• Depends on input (eg. already sorted or not)
• Depends on input size (-parameterize in input size)
• Want upper bounds

Kinds of analysis

Worst-case (usually)

　　T(n) = max time on any input of size n

Average-case (sometimes)

　　T(n) = expected time over all input of size n

　　(Need assumption of statistic distribution)

Best-case (bogus)

　　Cheat

What is insertion sort‘s worst time?

　　Depends on compater

　　　　——relative speed (on same machine)

　　　　——absolute speed (on different machine)

BIG IDEA!   —— asymptotic analysis

1. Ignore machine-dependent constants
2. Look at growth of the running time. T(n) as n → ∞

Asymptotic notation

θ - notation    Drop low-order terms and ignore leading constants

Ex. 3n³+90n²-5n+6046 = θ(n³)

As n → ∞, θ(n²) algorithm always beats a θ(n³) algorithm.

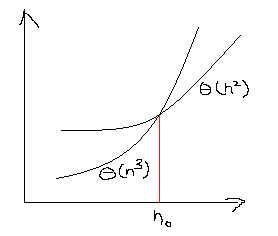Sometimes, n₀ may be too big so that a low-speed algorithm would be better.

Insertion Sort Analysis

Worst-case: input reverse sorted

T(n) = =θ(n²)

Is insertion Sort fast?

• Moderately so, for small n
• NOT at all for large n

Merge Sort Analysis

Merge sort A[1, ..., n]

1. If n = 1, done.       -------------------------- T(n)

2. Recursively sort      -------------------------- θ(1)

　　A[1, ..., n/2] and A[n/2 + 1, ..., n]   ----- 2T(n/2)

3. Merge 2 sorted list              ----------------- θ(n)

Key subroutine: Merge

For example, two sorted list:

2 7 13 20

1 9 11 12

compare 2 and 1, choose 1      [1]
comapre 2 and 9, choose 2      [1, 2]
comapre 7 and 9, choose 7      [1, 2, 7]
comapre 13 and 9, choose 9      [1, 2, 7, 9]
comapre 13 and 11, choose 11      [1, 2, 7, 9, 11]
comapre 13 and 12, choose 12      [1, 2, 7, 9, 11, 12]
put 13 and 20 to the end        [1, 2, 7, 9, 11, 12, 13, 20]

Time = θ(n) on n totoal elements

Recurrence

T(n) = θ(1), if n = 1    (usually omit it)

T(n) = 2T(n/2) + θ(n)

Recursive tree for T(n) = 2T(n/2) + cn

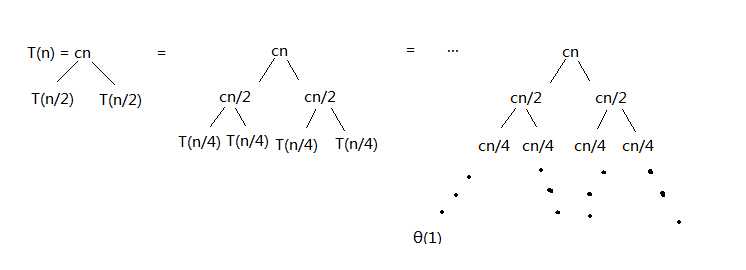
The height of this tree is lgn, the number of leavers is n, the subtotal of each depth is cn, So the total time is (cn)lgn+θ(n)

Omit the constant c and low-order θ(n), T(n) = θ(nlgn).

《算法导论》学习笔记一：课程简介及算法分析

标签：

原文地址：http://www.cnblogs.com/binarylu/p/4377024.html