标签:
题目:在原有的一位数组上进行扩展,求首尾相连的最大子数组的和:
要求: 输入一个一维整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。
结对编程要求: 两人结对完成编程任务。 一人主要负责程序分析,代码编程。
一人负责代码复审和代码测试计划。
发表一篇博客文章讲述两人合作中的过程、体会以及如何解决冲突(附结对开发的工作照)。
结对开发过程:
这次的编程开发是基于上次的以为数组,我和我的搭档@快乐的小菜鸟开始了认真的讨论,再结合课堂上的同学讨论,如何能在一维数组原有的基础上,加上首尾相连这个条件,同时降低时间复杂度,这种方法的大概思想是:遍历数组里面的每一个数将第一个数变为最后一个数,具体算法 a[i-1]=a[i],这样又变成了一个新的一维数组,输出每个数组的最大子数组和,然后比较每个输出的和,找出最大的数:
具体代码:
#include <iostream.h>
int maxSum(int* a, int n) //定义一个求一维数组的最大子数组和的方法
{
int sum=0;
int b=0;
for(int i=0; i<n; i++)
{
if(b<0)
b=a[i];
else
b+=a[i];
if(sum<b)
sum=b;
}
return sum;
}
int main()
{ int n,temp,b;
int sum=0;
int i;
int a1,a2;
cout<<"请输入数组的元素个数: "<<endl;
cin>>n;
cout<<"请输入数组的元素: "<<endl;
int *a=new int[n];
for( i=0;i<n;i++)
{cin>>a[i];}
cout<<"此首尾相连的数组中最大子数组的和有以下几种可能:"<<endl;
cout<<"第1种排列方式:"<<endl;
for( i=0;i<n;i++)
{cout<<a[i]<<" ";}
cout<<"最大子数组和为:"<<maxSum(a,n)<<endl;
a1=maxSum(a,n);
for(b=1;b<n;b++)
{
temp=a[0];
for(i=1;i<=n;i++)
{
a[i-1]=a[i];
}
a[n-1]=temp;
cout<<"第"<<b+1<<"种排列方式:"<<endl;
for( i=0;i<n;i++)
{cout<<a[i]<<" ";}
cout<<"最大子数组和为:"<<maxSum(a,n)<<endl;
if(maxSum(a,n)>=sum)
{sum=maxSum(a,n);}
}
a2=sum;
cout<<endl;
if(a1>=a2)
{cout<<"综上,最大的子数组和为:"<<a1<<endl;}
else
{cout<<"综上,最大的子数组和为:"<<a2<<endl;}
return 0;
}
截图:
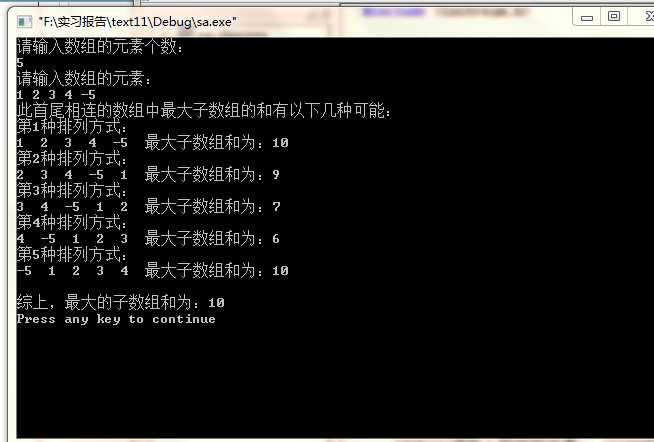
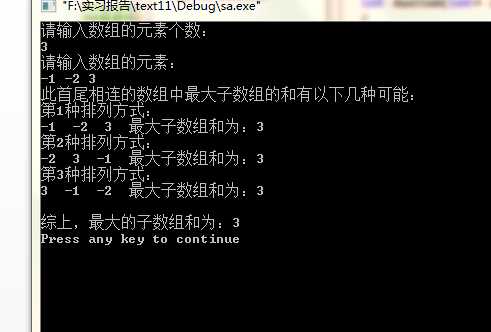
实验感想:
这次感觉题目算是比较简单,想通了其中的关键算法核心,就是a[i-1]=a[i],只不过算法复杂度可能不符合老师的要求!
结对伙伴截图:

标签:
原文地址:http://www.cnblogs.com/TSbj/p/4378707.html