标签:
要求输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建新的节点,只能调整树中结点指针的指向。
二叉树结点定义如下:
1 struct BinaryTreeNode 2 { 3 int m_nValue; 4 BinaryTreeNode *m_pLeft; 5 BinaryTreeNode *m_pRight; 6 };
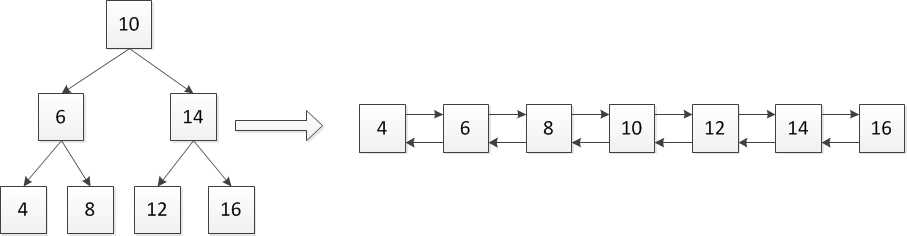
图1、二叉搜索树转为有序双向链表
因为二叉搜索树每个结点的子树也是一棵二叉搜索树,所以,我们可以把问题分解为,
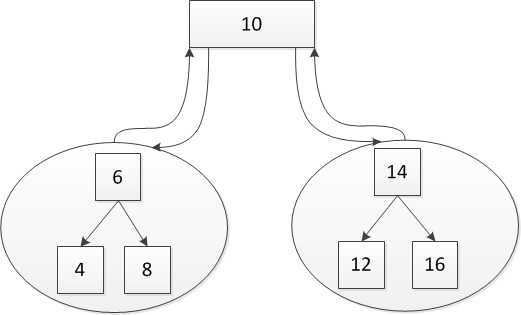
图2、分解为子问题
算法代码实现如下:
1 // 递归实现 2 3 void ConvertNode(BinaryTreeNode* pNode, BinaryTreeNode** pLastNodeInList) 4 { 5 if (pNode == NULL) 6 return; 7 8 BinaryTreeNode *pCurrent = pNode; 9 10 // 因为要求有序,所以先调整小的结点,也就是左子树的结点 11 if (pCurrent->m_pLeft != NULL) 12 ConvertNode(pNode->m_pLeft, pLastNodeInList); 13 14 // 此时左子树已经调整好,只需把当前结点和右子树的最后一个结点相连接即可 15 pCurrent->m_pLeft = *pLastNodeInList; 16 if (*pLastNodeInList != NULL) 17 (*pLastNodeInList)->m_pRight = pCurrent; 18 19 //此时当前链表中最后一个结点,已经变为当前结点了 20 *pLastNodeInList = pCurrent; 21 22 // 再调整右子树 23 if (pCurrent->m_pRight != NULL) 24 ConvertNode(pNode->m_pRight, pLastNodeInList); 25 26 } 27 28 BinaryTreeNode* Convert(BinaryTreeNode* pRoot) 29 { 30 BinaryTreeNode* pLastNodeInList = NULL; 31 ConvertNode(pRoot, &pLastNodeInList); 32 33 // pLastNodeInList指向双向链表的尾结点 34 // 我们需要返回头结点 35 BinaryTreeNode* pHeadOfList = pLastNodeInList; 36 while (pHeadOfList != NULL && pHeadOfList->m_pLeft != NULL) 37 pHeadOfList = pHeadOfList->m_pLeft; 38 39 return pHeadOfList; 40 }
上面的递归算法,虽然算法看起来比较好理解,但是由于需要不断的递归,导致不断的压栈,a、结点较多时有可能出现栈溢出;b、递归算法的多次压栈导致运行的时间效率较低。一般情况下,非递归算法要比递归算法有更好的时间和空间效率。
非递归算法的算法步骤:
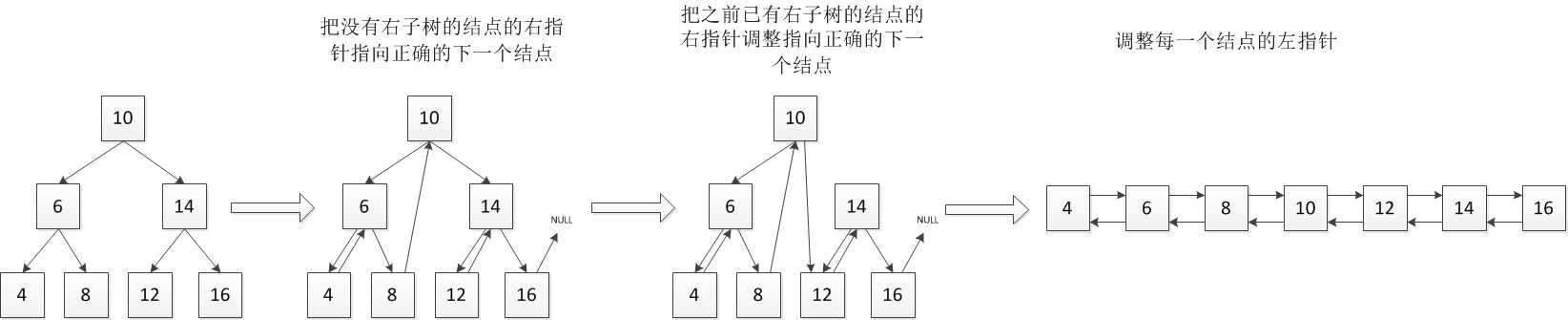
图3、非递归算法的算法步骤
算法的实现如下:
1 void AddRight(BinaryTreeNode* pCurrentNode, BinaryTreeNode* lastLeftAncestor) 2 { 3 if (pCurrentNode->m_pLeft != NULL) 4 AddRight(pCurrentNode->m_pLeft, pCurrentNode); // 从该节点往上回溯,第一个该节点的是其父节点的左孩子,lastLeftAncestor表示就是该节点的父节点 5 if (pCurrentNode->m_pRight == NULL) 6 pCurrentNode->m_pRight = lastLeftAncestor; //根据lastLeftAncestor的定义,其应该就是当前节点pRoot的在有序链表中的下一个节点 7 else 8 AddRight(pCurrentNode->m_pRight, lastLeftAncestor); 9 } 10 11 void AdjustRight(BinaryTreeNode* pCurrentNode) 12 { 13 if(pCurrentNode->m_pRight == NULL) 14 return; // 经过AddRight后,只有最右节点的m_pRight为NULL,如果m_pRight为空表示遍历结束 15 else 16 { 17 BinaryTreeNode* pNode = pCurrentNode->m_pRight->m_pLeft; 18 19 // 如果当前节点的右子树的做指针为空,那么pCurrentNode的右指针不需要修改 20 if (pNode == NULL) 21 return; 22 else 23 { 24 // 如果pCurrentNode的m_pRight指向正确的话,那么pCurrentNode一定是其m_pRight节点的左子树的最右节点 25 while(pNode->m_pRight != NULL && pNode != pCurrentNode) 26 pNode = pNode->m_pRight; 27 28 // 如果pCurrentNode的m_pRight指向正确的话,那么pCurrentNode一定是其m_pRight节点的左子树的最右节点 29 // 否则,通过不断访问m_pRight一定最后到达树的最右节点,即其右指针为NULL 30 // 此时需要调整当前节点的m_pRight为其右子树的最左节点 31 if(pNode->m_pRight == NULL) 32 { 33 pNode = pCurrentNode->m_pRight->m_pLeft; 34 while(pNode->m_pLeft != NULL) 35 pNode = pNode->m_pLeft; 36 37 // pCurrentNode的右指针调整为其右子树的最左节点 38 pCurrentNode->m_pRight = pNode; 39 } 40 } 41 } 42 } 43 44 void AdjustLeft(BinaryTreeNode* pCurrentNode) 45 { 46 if (pCurrentNode->m_pRight != NULL) 47 pCurrentNode->m_pRight->m_pLeft = pCurrentNode; 48 AdjustLeft(pCurrentNode->m_pRight); 49 } 50 51 BinaryTreeNode* Convert(BinaryTreeNode* pRoot) 52 { 53 if (pRoot == NULL) return NULL; 54 55 // 为无右子树的节点填写其右子树指针的值,其值为有序链表中该节点的下一个节点的地址 56 AddRight(pRoot, NULL); 57 58 BinaryTreeNode* pNode = pRoot; // pNode用于遍历 59 while (pNode->m_pLeft != NULL) 60 pNode = pNode->m_pLeft; 61 62 BinaryTreeNode* ListHead = pNode; // ListHead为有序链表的头,是二叉搜索树的最左节点 63 64 // Add后每个节点的右子树指针都不为空,除了最右节点 65 while (pNode->m_pRight != NULL) 66 { 67 AdjustRight(pNode); 68 pNode = pNode->m_pRight; 69 } 70 71 AdjustLeft(ListHead); 72 ListHead->m_pLeft = NULL; 73 return ListHead; 74 }
入口函数为Convert(BinaryTreeNode* pRoot),这个实现代码中其实还是有递归的,就是在最后调整左指针的时候,但是这个改为非递归,非常简单,所以我就没有去实现,算是一个不足吧。
标签:
原文地址:http://www.cnblogs.com/wangjzh/p/4380333.html