标签：

什么是插入排序？

插入排序的工作方式就像许多人排序一手扑克牌。开始的时候，我们的左手为空并且桌子上的牌面向下。然后我们每次从桌子上拿走一张牌并将它插入到左手中正确的位置。为了找到这张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较，如下图所示。那在左手上的牌总是排好序的，原来这些牌都是桌子上牌堆中顶部的牌。

插入排序伪代码

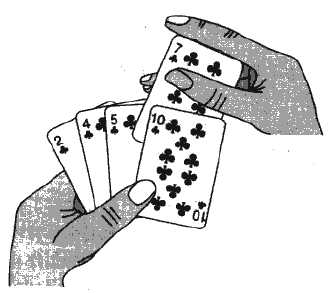
对于插入排序，我们将其伪代码过程命名为INSERTION-SORT[A]，其中的参数是一个数组A[1..n],包含长度为n的待排序的一个序列。下面为插入排序的不降序伪代码：

INSERTION-SORT(A)
1    for j = 2 to A.length
2        key = A[j]
3        //Insert A[j]into the sorted sequenceA[1..j - 1].
4        i = j - 1
5        while i > 0 and A[i]>key]
6            A[i + 1] = A[i]
7            i = i - 1
8        A[i + 1] = key

从上面的伪代码中我们不难看出插入排序的原理：

拿第i（i从2开始）个元素依次和它前面的元素做对比，由于是做不降序排序，只要发现前面的元素比第i个元素大,就将较大的那个元素往后移动一位，直到发现没有比它大的元素后停止比较并且把第i个元素插入到空出来的位置。无法理解的话在想想我们是怎么在手里排列扑克牌的。

插入排序的Java代码实现

 1     public int[] insertionSort(int[] array) {
 2 
 3         int key ;
 4         int i ;
 5         for(int j = 1; j < array.length; j++){
 6             key = array[j] ;
 7             i = j - 1 ;
 8             while(i >= 0 && array[i] > key){
 9                 array[i + 1] = array[i] ;
10                 i -- ;
11             }
12             array[i + 1] = key ;
13         }
14         return array ;
15 
16     }

循环不变式和插入排序的正确性

这里我们引入了一个比较新的概念“循环不变式”，那什么是循环不变式呢？

对于插入排序，经过j次循环后，数组中A[1..j-1]很显然是已经排好序的，随着循环次数的增多A[1..j-1]永远是排好序而不受循环次数的干扰。我们就把A[1..j-1]的这些性质形式的表示为一个循环不变式。

循环不变式主要用来帮助我们理解算法的正确性。关于循环不变式，我们必须证明三条性质：

初始化 ：循环的第一次迭代之前，它为真。

保持 : 如果循环的某次迭代之前它为真，那么下次迭代之前它仍然为真。

终止 ：在循环终止时，不变式为我们提供了一个有用的性质，该性质有助于证明算法是正确的。

 只要证明了以上三点，我们就可以证明我们算法的正确性。那么接下来我们就是这证明一下上面的三点：

1.初始化 首先证明在第一次循环迭代之前，循环不变式成立。实际上，第一次迭代之前，A[1..j-1]为A[1]，A[1]为排好序的这个显然是成立的。

2.保持 证明每次循环保持循环不变式，非形式化的证明，每次的for循环A[j-1],A[j-2],A[j-3]等向右移动一个位置，直到找到A[j]的适当位置，然后将A[j]插入该位置。这时候的数组由原先的A[1..j-1]和A[j]组成，并且此时A[j]已经处在一个正确的位置。所以A[1..j]是已经排好序的。所以对于每次循环，将保持循环不变式

3.终止 最后看看在循环终止的时候发生了什么？导致for循环终止的条件是j>A.length=n，因为每次循环迭代j增加1，那么必定有j = n + 1,在循环不变式的表述中我们将j用n+1代替，我们可以得到：子数组A[1..n]有原来在A[1..n]中的数组组成，但是已按序排列。我们注意到子数组A[1..n]就是整个数组，我们推断出整个数组已排序，因此算法正确。

【算法基础】插入排序

标签：

原文地址：http://www.cnblogs.com/zqlxtt/p/4381825.html