标签:
结对成员:信1201-1班 黄亚萍
信1201-1班 袁亚姣
一、题目要求
要求:
输入一个二维整形数组,数组里有正数也有负数。
二维数组首尾相接,象个一条首尾相接带子一样。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)题目:返回一个二维整数数组中最大子数组的和。
二、设计思路
类似于3,将二维数组转化为一维数组来求最大子数组的和,并输出其最大子数组。
三、程序源代码
1 #include <iostream> 2 #include <fstream> 3 using namespace std; 4 # define M 100 5 # define N 100 6 int hang1=0; 7 int hang2=0; 8 int lie1=0; 9 int lie2=0; 10 int maxx = -100; 11 int sum1(int k,int a[],int number) //一维数组行数元素求和 12 { 13 int x=0; 14 for(int i=k;i<=number+k-1;i++) //数组元素的个数为number 15 { 16 x=x+a[i]; 17 } 18 return x; 19 } 20 int sum2(int k,int a[M][N],int number,int num) //二维数组列数元素求和 21 { 22 int x=0; 23 for(int i=k;i<=number+k-1;i++) 24 { 25 x=x+a[i][num]; 26 } 27 return x; 28 } 29 int Largest1(int list1[],int length) //一维数组求数组的子数组的和的最大值 30 { 31 int sum[N]; 32 int i,j,max=-100; 33 for(i=1;i<=length;i++) //元素个数为i 34 { 35 for(j=1;j<=2*length-i;j++) //子数组的第j个元素,求最大值 36 { 37 sum[j]=sum1(j,list1,i); 38 if(sum[j]>=max) 39 { 40 max=sum[j]; 41 } 42 } 43 } 44 return max; 45 } 46 47 void Largest3(int list[],int length) 48 { 49 int sum[N]; 50 int i,j; 51 for(i=1;i<=length;i++) 52 { 53 for(j=1;j<=2*length-i;j++) 54 { 55 sum[j]=sum1(j,list,i); 56 if(sum[j]> maxx) 57 { 58 maxx=sum[j]; 59 lie1 = j; 60 lie2 = j+i-1; 61 } 62 } 63 } 64 } 65 66 int Largest2(int list[M][N],int number_x,int number_y) //二维数组求数组的子数组的和的最大值 67 { 68 int max,m; 69 int max2[N]; 70 int sum[M][N]; 71 int max3[N]; 72 for(int i=1;i<=number_x;i++) //数组行数为i 73 { 74 cout<<"子数组行数为"<<i<<","<<endl; 75 76 for(m=1;m<=number_x-i+1;m++) //子数组的第一行为原数组的第m行 77 { 78 cout<<" 第"<< m <<"行的最大值为:"; 79 for(int j=1;j<=2*number_y-1;j++) //子数组第j列元素 80 { 81 sum[i][j]=sum2(m,list,i,j); 82 } 83 Largest3(sum[i],number_y); 84 max2[m]=Largest1(sum[i],number_y); //数行数为i时子数组第m行的最大值 85 cout<<max2[m]<<endl; 86 max3[i]=max2[1]; 87 for(int k=1;k<=i;k++) 88 { 89 if(max2[k]>max3[i]) 90 { 91 max3[i]=max2[k]; 92 hang1=m; 93 } 94 } 95 } 96 } 97 max=max3[1]; 98 for(int n=1;n<=number_x;n++) 99 { 100 if(max3[n]>=max) 101 { 102 max=max3[n]; 103 hang1=m; 104 hang2=n; //子数组的行数为第m行到第m+n行 105 106 } 107 } 108 return max; 109 } 110 void show(int arry[N][N],int length1,int length2) //输出矩阵 111 { 112 for(int i=1;i<=length1;i++) 113 { 114 for(int j=1;j<=length2;j++) 115 { 116 cout<<arry[i][j]<<"\t"; 117 } 118 cout<<endl; 119 } 120 } 121 int main(int argc, char* argv[]) 122 { 123 int i,j,number_hang,number_lie; 124 int list[M][N],list1[M][N]; 125 126 ifstream infile("input.txt"); 127 if(!infile) 128 cout<<"读取失败!"<<endl; 129 else 130 { 131 infile>>number_hang>>number_lie; 132 for(int i=1;i<=number_hang;i++) 133 { 134 for(int j=1;j<=number_lie;j++) 135 { 136 infile>>list[i][j]; 137 } 138 } 139 } 140 141 cout<<"以矩阵形式展示为:"<<endl; 142 show(list,number_hang,number_lie); 143 cout<<endl; 144 145 cout<<"等价转换的数组为:"<<endl; 146 for(j=1;j<=number_hang;j++) 147 { 148 for( i=1;i<=2*number_lie-1;i++) 149 { 150 if(i<=number_lie) 151 { 152 list1[j][i]=list[j][i]; 153 } 154 else 155 { 156 list1[j][i]=list[j][i-number_lie]; 157 } 158 cout<<list1[j][i]<<" "; 159 } 160 cout<<endl; 161 } 162 163 164 cout<<"最大值为:"<<Largest2(list1,number_hang,number_lie)<<endl; 165 cout<<endl; 166 cout<<"对应的最大值的子数组为:"<<endl; 167 168 for(i=hang1-1;i<hang2+hang1-1;i++) 169 { 170 for(int j=lie1;j<=lie2;j++) 171 { 172 cout<<list1[i][j]<<"\t"; 173 } 174 cout<<endl; 175 } 176 cout<<endl; 177 return 0; 178 }
四、运行结果截图
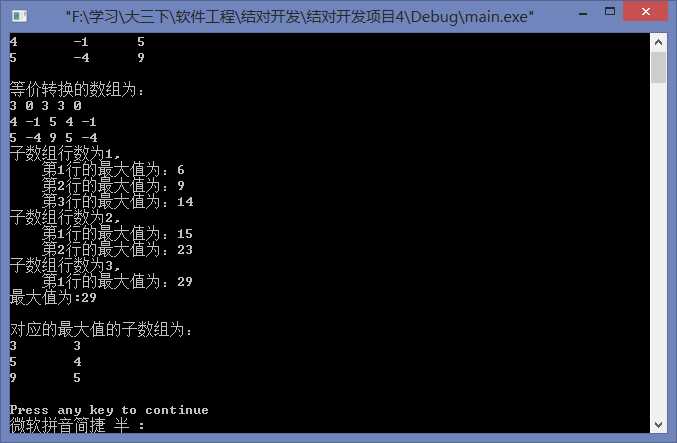
五、总结与心得
团队的细心与谨慎,以及思维的缜密是个人无法比拟的。当自己陷入迷茫时,队友的一个提醒与点播往往就能使我们豁然开朗。而队员之间的默契也会使我们的工作进展更加顺利。
标签:
原文地址:http://www.cnblogs.com/mudanhuakai/p/4384756.html