标签:
一、题目要求
输入一个二维整形数组,数组里有正数也有负数。
二维数组首尾相接,象个一条首尾相接带子一样。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。
要求时间复杂度为O(n)题目:返回一个二维整数数组中最大子数组的和
一、设计思想
求环形二维数组最大子数组的和,可以转化为求一维数组最大子数组的和
我们有一个最初的二维数组a[n][n]找它的 最大子数组之和
1.我们先建立一个新的二维数组b[n][2*n-1],
2,这个新的二维数组就是将初始的二维数组首尾相连,例如
数组a[0][0] a[0][1]首尾相连后变为a[0][0] a[0][1] a[0][0]
a[1][0] a[1][1] a[1][0] a[1][1] a[1][0]
2.循环:从a[0][0]开始 以此是 a[0][1]、 a[0][2]……a[0][m]、
a[1][0]、 a[1][1]……a[1][m]、
a[2][0]、 a[2][1]……a[2][m]、
……
a[n][0]、 a[n][1]……a[n][m]、
具体循环工作:当循环到a[j][k](0<=j<n,0<=k<m)则求的是 a[j][k]到 a[0][0] 的最大值
计算方法:根据b[j-1][k]、b[j][k-1]、b[j-1][k-1]的正负情况,来计算b[j][k],根据包含a[j][k]的各种矩阵情况,求得最大值。
3.求出b[m][n]中的最大值。
#include<iostream.h>
#include<conio.h>
int main()
{
int i,j;
int a[3][3];
int b[3][5];
int jixu;
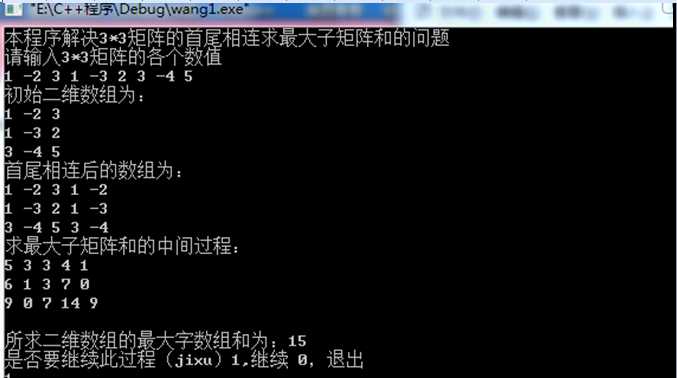
cout<<"本程序解决3*3矩阵的首尾相连求最大子矩阵和的问题"<<endl;
cout<<"请输入3*3矩阵的各个数值"<<endl;
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
cin>>a[i][j];
}
}
int max=a[0][0];
cout<<"初始二维数组为:"<<endl;
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
cout<<a[i][j]<<‘ ‘;
}
cout<<endl;
}
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
b[i][j]=a[i][j];
b[i][j+3]=a[i][j];
}
}
cout<<"首尾相连后的数组为:"<<endl;
for(i=0;i<3;i++)
{
for(j=0;j<5;j++)
{
cout<<b[i][j]<<‘ ‘;
}
cout<<endl;
}
for(i=0;i<1;i++)
{
b[0][0]=a[0][0];
for(j=0;j<5;j++)
{
if(a[0][j-1]<0)
{
b[0][j]=a[0][j];
}
else
{
b[0][j]=b[0][j-1]+a[0][j];
}
}
}
for(i=1;i<3;i++)
{
for(j=0;j<1;j++)
{
if(a[i-1][0]<0)
{
b[i][0]=a[i][0];
}
else
{
b[i][0]=b[i-1][0]+a[i][0];
}
}
}
for(i=1;i<3;i++)
{
for(j=1;j<5;j++)
{
if(b[i-1][j-1]<0)
{
if(b[i-1][j]>=0&&b[i][j-1]>=0)
{
if(b[i][j-1]>=b[i-1][j])
{
b[i][j]=b[i][j-1]+a[i][j];
}
else
{
b[i][j]=b[i-1][j]+a[i][j];
}
}
else if(b[i-1][j]>=0&&b[i][j-1]<=0)
{
b[i][j]=b[i-1][j]+a[i][j];
}
else if(b[i-1][j]<=0&&b[i][j-1]>=0)
{
b[i][j]=b[i][j-1]+a[i][j];
}
else
{
b[i][j]=a[i][j];
}
}
else
{
if(b[i-1][j]>=0&&b[i][j-1]>=0)
{
b[i][j]=a[i][j]+b[i-1][j]+b[i][j-1]-b[i-1][j-1];
}
else if(b[i-1][j]>=0&&b[i][j-1]<=0)
{
b[i][j]=a[i][j]+b[i-1][j]-b[i-1][j-1];
}
else if(b[i-1][j]<=0&&b[i][j-1]>=0)
{
b[i][j]=a[i][j]+b[i][j-1]-b[i-1][j-1];
}
else
{
b[i][j]=a[i][j];
}
}
}
}
cout<<"求最大子矩阵和的中间过程:"<<endl;
for(i=0;i<3;i++)
{
for(j=0;j<5;j++)
{
cout<<b[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
for(i=0;i<3;i++)
{
for(j=0;j<5;j++)
{
if(b[i][j]>max)
max=b[i][j];
}
}
cout<<"所求二维数组的最大字数组和为:"<<max+1<<endl;
cout<<"是否要继续此过程(jixu)1,继续 0,退出"<<endl;
cin>>jixu;
if(jixu==1)
{
cout<<endl;
main();
}
else
{
return 0;
}
getch();
return 0;
}
总结:这次我和小伙伴互换了角色,我负责敲代码,小伙伴负责代码审查,因为有了前几次结对开发的经验,这次任务进行的比较顺利。在上一次求二维数组子数组和的最大值时,查阅了很多资料,因此思路比较宽阔,在上一次大代码上经过简略的修改,就完成了这次的任务。通过互换角色,也发现了以往掩饰的不足,看到了对方的长处。希望以后能够合作更加愉快。

标签:
原文地址:http://www.cnblogs.com/xiaojin123/p/4391057.html