树状数组

标签：

序：说起树状数组,记得这是我正式去组里的第一天，一点基础都没有的我顿时就懵了，学长在上面讲，完全不知所云，于是那天晚上就失眠了。。。

正文：

    一 树状数组就是给你一个数组int a[N],对这个数组进行如下操作：

      （1）修改数组中某元素的值；

      （2）查询该数组任意区间的和。

        任何算法都是以减少复杂度为目的的。其复杂度为（M+Q）log2(N）;

        （M为修改次数，Q为查询次数，N为数组长度）

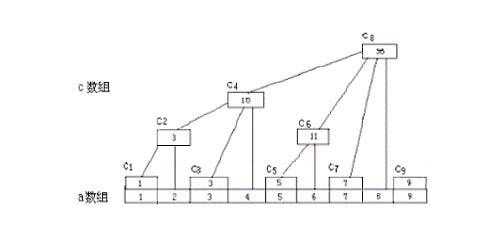
      首先设一个C数组构成一个树状关系：C[x]分布在 log2(lowbit(x)) 层；每个C[k]只有一个父亲节点，子节点与其父节点之间的距离为lowbit(k)。

      对（1）操作，修改某位置k的值，则对于数组C要修改包括a[k]的位置，k与下一个节点的距离为lowbit(k)。

      对（2）操作，查询某位置k的sum(k)，则一次查询包括k到1的sum，k与其下一个相关节点的位置的距离为lowbit(k)。

     函数实现代码：

int lowbit(int x)   //位运算求lowbit(x)
{
    return x&(-x);
}

int getsum(int x)     //求sum
{
    int result=0;
    while(x>0)
   {
    result +=c[x];
    x-=lowbit(x);
   }
   return result;
} 

void add(int x)      //修改位置为x的值，val为变化值，可为+-；
{
      while(x<=Max)
      {
        c[x]+=val;
        x+=lowbit(x);
       }
}

View Code

     也可构造二维数状数组

int lowbit(int x)
{
   return x&(-x);
}

void add(int x,int y,int val)
{
   int i,j;
   for(i=x;i<=n;i+=lowbit(i))
   for(j=y;j<=n;j+=lowbit(j))
   c[i][j]+=val;
}

int getsum(int x,int y)
{
   int i,j,sum=0;

   for(i=x;i>0;i-=lowbit(i))
   for(j=y;j>0;j-=lowbit(j))
   sum+=c[i][j];
   return sum;
}

View Code

   二 应用

    （1）假如给定一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[1],a[2]...a[i-1]中(即位 置i的左边)小于等于a[i]的数的个数。对此例b[] = {0,1,1,2,0}。 那么该如何去求得b[i]呢？

    （2）假如给你一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[1],a[2]...a[i-1]中(即位置i的左边)大于等于a[i]的数的个数。对此例b[] = {0,0,1,1,4}。 那么该如何去求得b[i]呢？

    （3）假如给你一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[i],a[i+1]...a[n]中(即位置i的右边)小于等于a[i]的数的个数。对此例b[] = {1,3,1,1,0}。 那么该如何去求得b[i]呢？

    （4）假如给你一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[i],a[i+1]...a[n]中(即位置i的右边)大于等于a[i]的数的个数。对此例b[] = {3,0,1,0,0}。 那么该如何去求得b[i]呢？

      以上四种情况殊途同归，其中（2）可以将其编号倒过来用（1）的方法求；

                                          （4）可以将其编号倒过来用（3）的方法求。

       用数状数组函数调用方式

for(int i=1; i<=n; i++)
{
     b[i] = getSum(a[i]); //求前a[i]项的和
    update(a[i],1);      //第a[i]个元素+1
}

View Code

     虽然现在稍懂了一点，但是还是应用不好，不过吾将上下而求索。

树状数组

标签：

原文地址：http://www.cnblogs.com/searchmushan/p/4396560.html