二维数组-最大子数组

标签：

一 题目:求二维数组中最大子数组的和

二 设计思路

      我认为若想求二维数组中最大子数组，可以将二维数组化为一维数组，在对其求连续子数组最大值。那么如何将一个二维数组化为一维数组呢?可以举一个例子，如下:

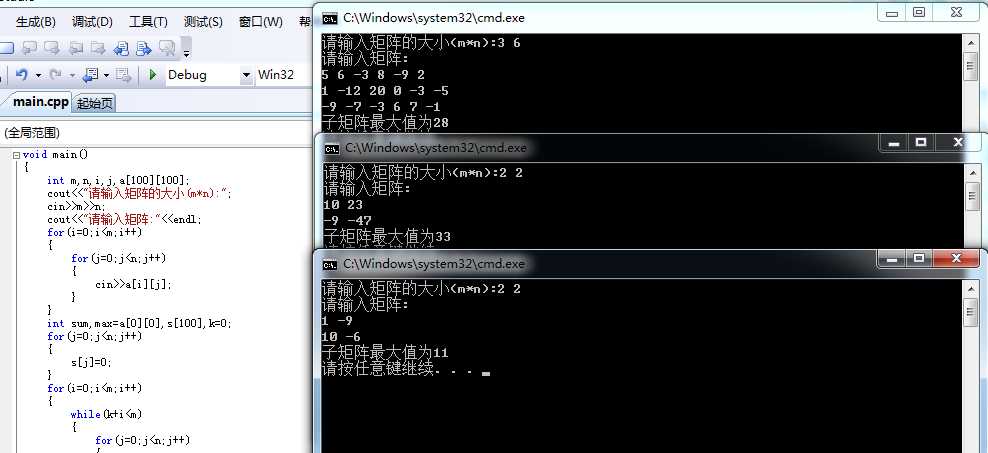
i=0   5    6  -3   8  -9   2

i=1  1   -12   20  0   -3  -5

i=2   -9  -7  -3  6   7   -1

例子为一个3*6矩阵，令其为a[3][6]。由于可以行行相加或列列相加转化为一维数组，在这为行行相加，故附设一个一维数组是s[6]，初值均为0。附设两变量SUM和MAX，max初始值为a[0][0]即5。当i=0时，将a[0][0]-a[0][5]的值赋给s[6]，用求一维最大子数组的方法求得最大值赋给MAX，然后，再将i=1行的元素加到第一行(即s[j]=s[j]+a[1][j])再赋值给s[6]，求最大子数组，然后接着将第三行元素往上加(即s[j]=s[j]+a[2][j]),最后求得含第一行元素的子矩阵的最大值。把s[6]回归为0。同理，从第二行开始，依次往下加，从第三行开始....最后可求得最大子矩阵的值。这种算法的时间复杂度为O(n^3).

三 代码实现

#include<iostream>
using namespace std;

void main()
{
     int m,n,i,j,a[100][100];
     cout<<"请输入矩阵的大小(m*n):";
     cin>>m>>n;
     cout<<"请输入矩阵:"<<endl;
     for(i=0;i<m;i++)
    {
          for(j=0;j<n;j++)
         {
                cin>>a[i][j];
          }
     }
     int sum,max=a[0][0],s[100],k=0;
     for(i=0;i<m;i++)
    {
           while(k+i<m)
          {
                 for(j=0;j<n;j++)
                {
                       s[j]=s[j]+a[k+i][j];
                }
                sum=0;
                for(j=0;j<n;j++)
                {
                       if(s[j]+sum>s[j])
                       {
                               sum=s[j]+sum;
                       }
                       else
                       {
                               sum=s[j];
                       }
                       if(sum>max)
                       {
                               max=sum;
                       }
                 }
                 k++;
           }
           k=0;
           for(j=0;j<n;j++)
          {
                 s[j]=0;
           }
      }
           cout<<"子矩阵最大值为"<<max<<endl;
}

四 截图

二维数组-最大子数组

标签：

原文地址：http://www.cnblogs.com/houtaoliang/p/4401630.html