标签:
堆的数据结构是一种数组对象;堆可以视作为一颗完全二叉树(其中,树的每一层都填满,最后一层可能除外);树中每个节点与数组中存放该节点值的元素对应;
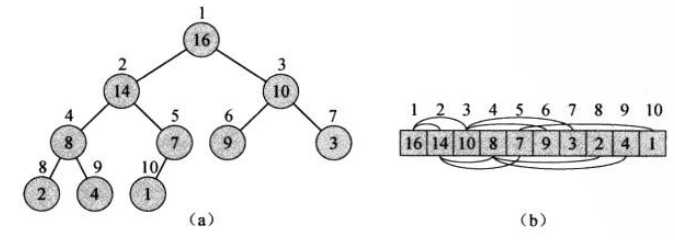
堆可以划分为两类:
a) 最大堆:除了根节点,有A[parent(i)] >= A[i],最大元素即根节点;
b) 最小堆:除了根节点,有A[parent(i)] <= A[i],最小元素即根节点;
对于给定节点i,可以根据其在数组中的位置求出该节点的父亲节点PARENT(i)=i/2、左孩子LEFT(i) = 2*i和右孩子RIGHT(i) = 2*i+1节点,这三个过程一般采用宏或者内联函数实现。
1 #define LEFT(i) (2 * i) 2 #define RIGHT(i) (2 * i + 1)
把堆看成一个棵树,有如下的特性:
a) 含有n个元素的堆的高度是lgn。
b) 当用数组表示存储了n个元素的堆时,叶子节点的下标是n/2+1,n/2+2,……,n
c) 在最大堆中,最大元素该子树的根上;在最小堆中,最小元素在该子树的根上。
划分为三块:保持堆性质、创建堆、排序;
1) 保持堆性质
通过MAX_HEAPIFY()函数,使得堆把持最大堆的性质,即除了根节点,有A[parent(i)] >= A[i],具体如下:
标签:
原文地址:http://www.cnblogs.com/syd192/p/4401764.html