标签:
题目:返回一个二维整数数组中最大子数组的和。
要求:输入一个二维整形数组,数组里有正数也有负数。
二维数组中连续的一个子矩阵组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
结对编程要求:两人结对完成编程任务。
一人主要负责程序分析,代码编程。
一人负责代码复审和代码测试计划。
发表一篇博客文章讲述两人合作中的过程、体会以及如何解决冲突(附结对开发的工作照)。
编程思路:(在网上搜索的程序代码和思路,我们对其进行整理得到现在的思路)先宏定义m和n,分别为二维数组的行数和列数,在主函数中定义一个整型的二维数组,二维数组的元素由随机生成函数rand()生成,对于生成的二维数组,我们先计算出第一行中有关第一个元素的所有子数组,然后计算出第二个第三个直到第n个,第二行第三行直到第m行同第一行,把上面计算出来的子数组存放在另一个二维数组里,再求这个二维数组的子数组的最大值(根据列数来求),定义一个变量max(二维数组中最大子数组的和),把max的值赋为0,把从另一个二维数组得到的最大值和max比较,以此类推,最后即可得到最大子数组的和。
源程序代码:
#include <iostream>
#define m 4
#define n 3
using namespace std;
int main()
{
int a[m][n];
int max;
int s;
int count;
int b[m][m];
cout<<"该二维数组为:"<<endl;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
a[i][j]=rand()%100-50;
cout<<a[i][j]<<" ";
}
cout<<endl;
}
for(int i=0;i<m;i++)
{
count=0;
for(int j=0;j<n;j++)
{
s=0;
for(int l=0;l<n-j;l++)
{
s=s+a[i][j+l];
b[i][count+l]=s;
}
count=count+n-j;
}
}
//求最大数
max=b[0][0];
for(int j=0;j<m;j++)
{
for(int i=0;i<m;i++)
{
s=0;
for(int r=0;r<m-i;r++)
{
s=s+b[r+i][j];
if(max<s)
max=s;
}
}
}
cout<<"最大子数组的和为:"<<max<<endl;
return 0;
}
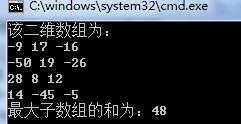
测试结果:
孟祥娟:主要负责代码复审和代码测试计划;
陈杰:主要负责程序分析,代码编程。
合作照片:
总结:在一个程序里面最重要的就是编程思路,思路非常重要,还有就是代码的规范性;
标签:
原文地址:http://www.cnblogs.com/chenjie00/p/4403677.html