LMS算法去噪

标签：

LMS在语音增强中具备广泛的应用，是最为常见的算法之一，该算法也是很多更为复杂算法的理论基础或 组成部分，例如阵列语音增强中的重要方法--GSC（广义旁瓣抵消）。LMS算法由最初的版本延伸出来许多变种结构，例如归一化LMS，变步长LMS等等。这些都是对LMS的迭代部分进行了一定的优化所得。

最近又看起了GSC的实现，以前写的程序又重新看了一遍，差不多又巩固了一遍，希望以后自己能够不要忘记了····我这个破记性，有时候真是很无奈！

首先是理论部分推导，在此不详述，简要给出流程：

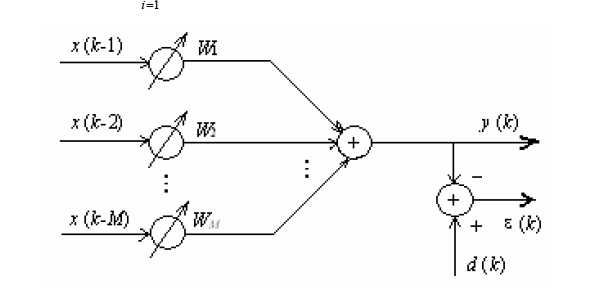
                                自适应线性组合器及LMS原理图

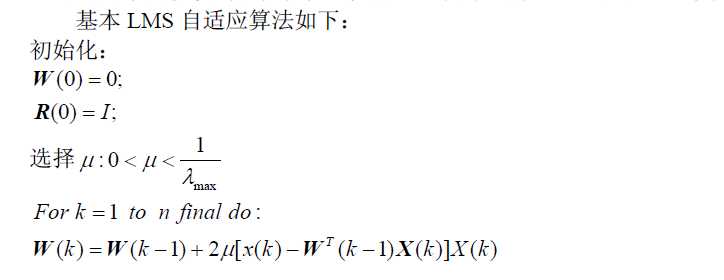
MATLAB实现程序如下（变步长LMS）：

clear;%清除工作空间
close all%...
sysorder=5;%抽头数...
samples_per_period=50; %周期采样频率
N=10*samples_per_period-1;%总采样次数
signal=cos(pi*0.02*[0:N-1])+sin(2*pi*0.02*[0:N-1])+cos(3*pi*0.02*[0:N-1])+sin(4*pi*0.02*[0:N-1])+cos(5*pi*0.02*[0:N-1])...
     +sin(6*pi*0.02*[0:N-1])+cos(7*pi*0.02*[0:N-1])+sin(8*pi*0.02*[0:N-1])+cos(9*pi*0.02*[0:N-1]);%初始输入信号/期望信号
figure()    %作图1 的第一子图
subplot(2,1,1);
 plot(signal);
 grid;
 title(‘自适应滤波器的理想输入‘);
nvar=0.5;%噪声方差
noise=nvar*randn(1,N );%噪声信号
X=signal+noise;%带加性噪声的输入信号
delayX=[0 X];% 输入信号延时
subplot(2,1,2);%作图1的第二子图
plot(delayX);
 grid;
 title(‘自适应滤波器的噪声输入‘);
SIGNAL=[signal 0];
 %M=32;%滤波器长度
M=length(signal);%M为接收数据长度
mu=0.002;%迭代步长
totallength=size(X,1);%步长
N=size(signal,2);%60结点作为训练序列
%算法的开始
w=zeros(sysorder,1);%初始化
for n=sysorder:N
    y(1:sysorder)=X(1:sysorder);  % 前五个值赋为原始值
    y(n)=X(n-sysorder+1:1:n)*w;  %系统输出
    e(n)=y(n)-signal(n);  %系统误差
    if n<200
         mu=0.0032;
     else
         mu=0.0015;
    end
     step=mu./(1+abs(e(n)).^2);
     w=w+step*X(n:-1:n-sysorder+1)‘*e(n);%迭代方程
end
Y=-y;
 %initial_status=initlms(zeros(1,M),mu);%滤波器设初值
%[Y,e,initial_status]=adaptlms(X,SIGNAL,initial_status);%LMS自适应滤波器输出
figure()    %作图2的第一子图
subplot(2,1,1);
 plot(0:N-1,Y,‘r‘,1:N ,signal,‘b‘);
 grid;
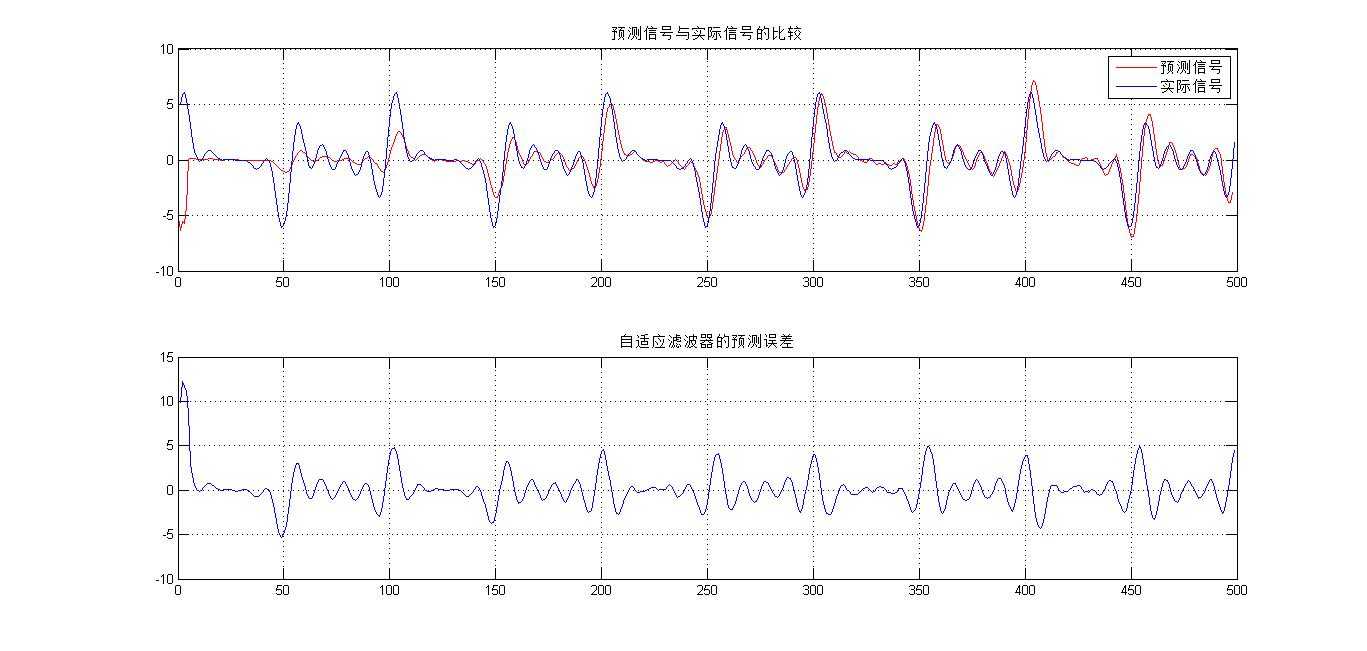
 title(‘预测信号与实际信号的比较‘);
legend(‘预测信号‘, ‘实际信号‘);
error=signal-Y;%输出误差信号
subplot(2,1,2);%作图2的第二子图
plot(error);
 grid;
 title(‘自适应滤波器的预测误差‘);

所得仿真跟踪滤波图形结果示意图如下所示，可见预测信号在LMS收敛之后能够较好的跟踪实际信号的变换，且去除了其中的噪声信号（含噪信号在此未贴图）。其中预测误差由信号未对齐所引起，程序中引入了一个延时所致：

LMS算法去噪

标签：

原文地址：http://www.cnblogs.com/Martin-Ma/p/4413357.html