标签:
本文只使用他人托管的jar包,不涉及具体算法
软件测试通常要花费掉软件开发组织30%~70%的开发资源,如何有效地提高软件测试的效率是开发组织应该考虑的关键问题之一。由于很多情况下穷举测试是不可行的,测试人员必须在时间和资源的有限性与测试覆盖的彻底性之间做好权衡。解决这个问题的一个行之有效的方法便是Pairwise Testing。
一、Pairwise Testing
先举例子
在测试用例设计过程中,有时会遇到很多变量进行组合的情况,对相互组合的两个或更多变量进行的测试活动就是组合测试,比如
操作系统:Win98,Win2K,WinXP 打印机:HP 4050,HP 4100 双工:Y,N
完全测试需要包括所有这些参数的排列组合:
CASE OS 打印机 双工 1 Win98 HP 4050 Y 2 Win98 HP 4100 Y 3 Win2K HP 4050 Y 4 Win2K HP 4100 Y 5 WinXP HP 4050 Y 6 WinXP HP 4100 Y 7 Win98 HP 4050 N 8 Win98 HP 4100 N 9 Win2K HP 4050 N 10 Win2K HP 4100 N 11 WinXP HP 4050 N 12 WinXP HP 4100 N
利用Pairwise Testing,测试用例可以简化成:
CASE OS 打印机 双工 1 Win98 HP 4050 Y 2 Win98 HP 4100 N 3 Win2K HP 4050 N 4 Win2K HP 4100 Y 5 WinXP HP 4050 Y 6 WinXP HP 4100 N
组合测试(Combinatorial Test)是一种测试用例生成方法。它将被测试应用抽象为一个受到多个因素影响的系统,其中每个因素的取值是离散且有限的。两因素(Pairwise)组合测试生成一组测试用例集,可以覆盖任意两个因素的所有取值组合,在理论上可以暴露所有由两个因素共同作用而引发的缺陷。多因素(N-way,N>2)组合测试可以生成测试用例集,以覆盖任意N个因素的所有取值组合,在理论上可以发现由N个因素共同作用引发的缺陷。由于两因素组合测试在测试用例个数和错误检测能力上达到了较好的平衡,它是目前主流的组合测试方法。
成对测试(Pairwise Testing),是一种有效的测试用例生成技术,通过对测试变量的所有维度及值的组合,避免穷举测试所有维度的所有值及其组合来减少测试用例数量。
成对测试这一概念是Mandl于1985年在测试Aad编译程序时提出来的。Cohen等人应用成对组合覆盖测试技术对Unix中的“Sort”命令进行了测试。测试结果表明覆盖率高达90%以上。可见成对组合覆盖是一种非常有效的测试用例设计方法。
为了更好地理解其概念本身,首先引入几个相关概念的介绍。因素,就是影响软件行为的参数或变量;水平,就是某个因素的可能取值;强度,就是因素之间相互关系的程度,取值为二时只考虑两两因素的取值对软件行为的影响,取值为三时考虑任意三个因素的取值对软件行为的影响;次数,就是所产生的测试用例的个数。
因为“大多数故障是由最多两个因素相互作用引起的”,Pairwise Testing便是强度为二的情况,其要求任意两个因素的所有水平之间的组合至少要被覆盖1次,生成的测试用例可以保证各个因素每个水平之间的两两组合至少出现一次。在因素和水平的数量很大时,Pairwise Testing对测试用例的精简效果显著。成对测试的算法已经被很多工具实现,例如:TConfig、微软的PICT等。
Pairwise Testing有一个官网:http://www.pairwise.org/
其中包括大量Pairwise Testing工具:http://www.pairwise.org/tools.asp
目测其中的大多数链接都需要科学上网,最有名的是PICT。
二、Pairwise Testing 的数学基础
Pairwise Testing具有严谨的数学基础——正交表。
不要使用正交表,要使用PICT。
有一些文章介绍了利用正交表构造组合测试用例集的方法。虽然可行,但是正交表并不是理想的组合测试工具。
首先,正交表的性质并不适用于软件测试。正交表是为正交试验服务的,它求对任意两个因素的取值组合实施“等概率”覆盖,以便实验样本“均匀”地分布在样本空间。“等概率覆盖”有助于在正交试验中确定各个因素对实验结果的贡献,但是对于组合测试提高错误检测能力并没有帮助。受到“等概率覆盖”的约束,正交表往比“覆盖即可”的组合测试工具生成更多的测试用例,提高了测试成本。
第二,利用正交表构造组合测试用例并不方便。使用正交表构造测试用例,要寻找正确的正交表、对其进行剪裁、替换参数,方能获得测试用例集。如果使用微软提供的组合测试工具PICT,生成测试用例会非常简单。
三、PICT工具
PICT(Pairwise Independent Combinatorial Testing )原是微软公司内部使用的一款自动生成成对组合测试用例的命令行工具,现在对外提供,可以从互联网上下载到。
PICT微软相关:http://blogs.msdn.com/b/testercenter/
PICT下载地址:http://download.microsoft.com/download/f/5/5/f55484df-8494-48fa-8dbd-8c6f76cc014b/pict33.msi
PICT可以有效地按照两两测试的原理,进行测试用例的设计。在使用PICT时,需要输入与测试用例相关的所有参数,以达到全面覆盖的效果
1.模型文件
PICT接收一个纯文本文件作为输入,然后输出测试用例集合。在文本文件中描述被测试应用的模型(Model),即该软件有哪些因素、每个因素有哪些取值。该文本文件被称为模型文件。格式如下:
<ParamName1> : <Value1>, <Value2>, <Value3>, ...
<ParamName2> : <Value1>, <Value2>, <Value3>, ...
例如:将文本文件保存为test.txt,保存在E:\PICT\
OS:Win8,Win7,WinXP,Linux,MacOS 数据库:Oracle,MySQL,SQLServer,Access JDK:1.8.0,1.7.0,1.6.0,1.5.0 字符集:utf-8,GBK
2.运行PICT程序
命令行:
E:\PICT>pict test.txt
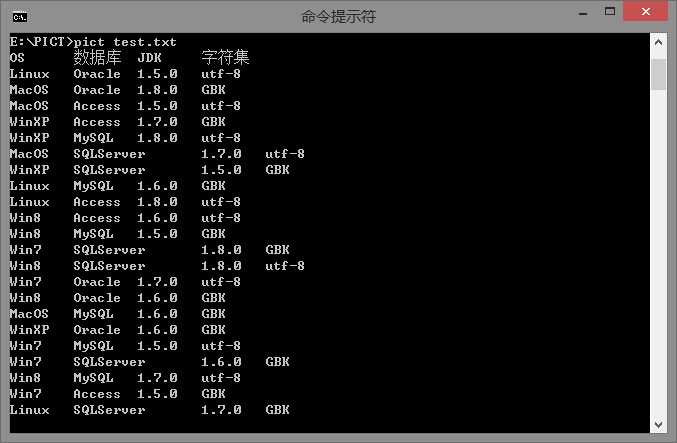
可以将结果输出保存至txt和xls文件:
E:\PICT>pict test.txt > Output.txt
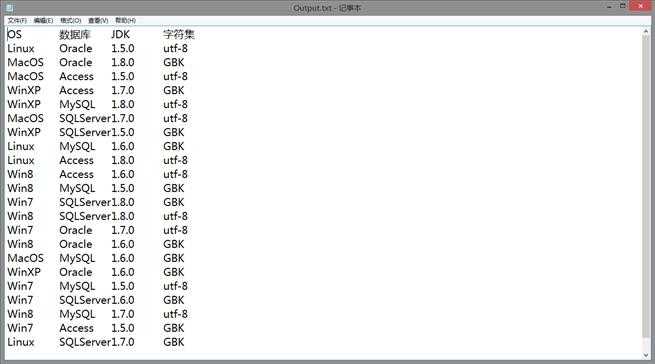
E:\PICT>pict test.txt > OutputFile.xls
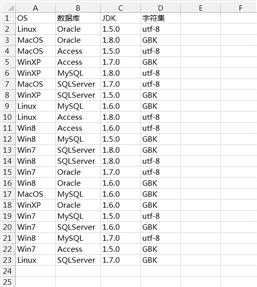
3.PICT选项
/o:N 组合数,默认值为2,即pict生成的测试用例集中每条测试数据会有两个值与其他测试集是不同的;
/d:C 值与值之间的分隔符,默认为逗号(,),例如一个参数 操作系统 winxp,win7,win8 之间会用逗号隔开;
/a:C 别名间的分隔符,默认是管道符(|),例如一个参数(用户名不区分大小写,但为了保证测试的可信度,可以用大小写轮换的方式进行测试) 用户名 admin|ADMIN;
/n:C 无效数值或者是非法数值的前缀,默认值为(~),例如一个参数(只能取1、2,为了测试非法值的输入,取0,但又不希望0和其他参数的每隔值都配一次对,为了减少测试集的数量,在0前面加一个~)即 参数 ~0,1,2;
/e:file 定义种子文件,作用是可以指定组合方式,例如在种子文件seed.txt中指定一个组合方式,在执行1.txt时,命令:pict 1.txt /e:seed.txt 生成的测试集中会包含seed中指定的组合集(当然指定的组合集有一定条件)。(此参数目前的理解可能会有误区);
/r[:N] 通过/r参数,可以使每次生成的测试集不同;
/c 加上该参数,说明参数值完全区分大小写
/s 显示模型统计数据
4.PICT的更多细节
关于PICT有更多复杂的用法,可查看PICT的帮助文档,还可参考
Liang Shi 实施组合测试 http://www.cnblogs.com/liangshi/archive/2010/07/25/1784666.html
Wade Xu 具有约束关系的因素如何实施组合测试 http://www.cnblogs.com/wade-xu/p/4220496.html
四、Pairwise Testing 的Java实现
1.Pairwise Testing Service
有关Pairwise Testing的具体算法网上的资料少的可怜,我只找到一个Pairwise Testing Service项目托管在Google Code上
http://code.google.com/p/pairwisetestingservice/source/browse
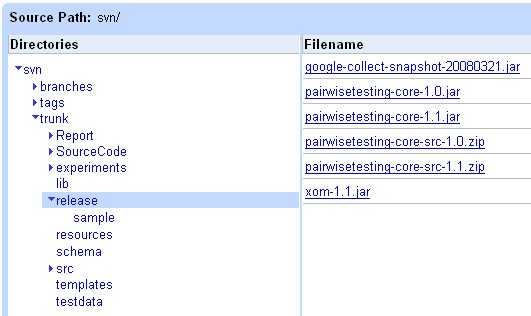
此项目对Pairwise Testing介绍的极为详细,其中有核心包和源码,还有一个Construction Orthogonal Arrays.ppt和一个Pairwise Testing - Orthogonal Arrays Strategy.doc文件,详细介绍了Pairwise Testing的数学基础与实现方法。另外,这个项目是中国程序员写的,在此对作者表示崇高的敬意。
Google Code 快要关了,我把 Pairwise Testing Service 中的部分文件存在了我的网盘里:http://pan.baidu.com/s/1dDo3t7r
2.Pairwise Testing Service 算法
Pairwise Testing是个大家族,按照所基于的理论背景不同,可以分为计算机科学的方法和数学的方法两大类。计算机科学的方法都是基于启发式算法,不能得到最优解,典型代表是Jenny、PICT和TVG。数学方法的典型代表是正交表,虽然能在一些特定的场合得到最优解,但受限于数学基础的理论限制而无法应用于所有场合。
Pairwise Testing Service便是基于正交表的Pairwise Testing。
也就是说,Pairwise Testing Service的算法与其他PICT等软件是不同的!
启发式算法(heuristic algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。启发式算法可以这样定义:一个基于直观或经验构造的算法,在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解,该可行解与最优解的偏离程度一般不能被预计。计算机科学的两大基础目标,就是发现可证明其执行效率良好且可得最佳解或次佳解的算法。而启发式算法则试图一次提供一或全部目标。 例如它常能发现很不错的解,但也没办法证明它不会得到较坏的解;它通常可在合理时间解出答案,但也没办法知道它是否每次都可以这样的速度求解。有时候人们会发现在某些特殊情况下,启发式算法会得到很坏的答案或效率极差,然而造成那些特殊情况的数据组合,也许永远不会在现实世界出现。因此现实世界中启发式算法常用来解决问题。启发式算法处理许多实际问题时通常可以在合理时间内得到不错的答案。
3.Pairwise Testing Service 使用
我们使用如下例子

pairwisetesting.jar 需要 XOM 和 Google Collections。首先在java项目中包含pairwisetesting-core-1.1.jar,xom-1.1.jar,google-collect-snapshot-20080321.jar
创建PairwiseTesting.java
import pairwisetesting.PairwiseTestingToolkit; import pairwisetesting.coredomain.*; import pairwisetesting.engine.am.AMEngine; import pairwisetesting.testcasesgenerator.TXTTestCasesGenerator; public class PairwiseTesting { public static void main(String[] args) throws Exception { PairwiseTestingToolkit toolkit = new PairwiseTestingToolkit(); // 设置元参数提供者 toolkit.setMetaParameterProvider(new IMetaParameterProvider() { public MetaParameter get() { // 创建因素及其水平值 Factor f1 = new Factor("用户星级"); f1.addLevel("一星"); f1.addLevel("二星"); f1.addLevel("三星"); Factor f2 = new Factor("用户类型"); f2.addLevel("普通用户"); f2.addLevel("学生"); f2.addLevel("内部员工"); Factor f3 = new Factor("包装方式"); f3.addLevel("普通包装"); f3.addLevel("加固包装"); f3.addLevel("礼品包装"); // 强度为2 MetaParameter mp = new MetaParameter(2); mp.addFactor(f1); mp.addFactor(f2); mp.addFactor(f3); return mp; } }); // 使用AMEngine toolkit.setEngine(new AMEngine()); // 使用文本输出的测试用例生成器 toolkit.setTestCasesGenerator(new TXTTestCasesGenerator()); System.out.println(toolkit.generateTestCases()); } }
运行后得到输出
用户星级 用户类型 包装方式
一星 普通用户 普通包装
一星 学生 加固包装
一星 内部员工 礼品包装
二星 普通用户 加固包装
二星 学生 礼品包装
二星 内部员工 普通包装
三星 普通用户 礼品包装
三星 学生 普通包装
三星 内部员工 加固包装
4.Pairwise Testing Service 详细介绍
以下文本直接复制自Pairwise Testing - Orthogonal Arrays Strategy.doc
在综合实践项目中,我们将正交表的理论应用于Pairwise Testing Service的开发中,集中体现在AMEngine(Algebra Method Engine)的设计与实现中。Pairwise Testing Service中有很多其它Engine,下图所示的是AMEngine所处的位置。
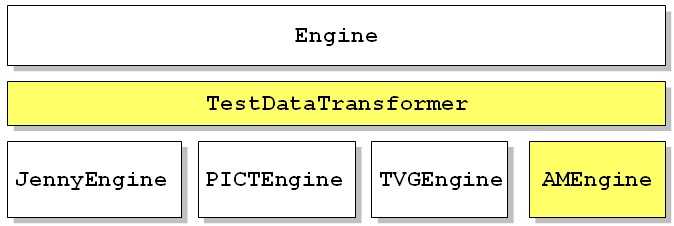
TestDataTransformer是几乎每个Engine都要自定义的转换器,特别是对AMEngine,其原生的测试数据只是些数字,需要转换成用户友好的信息展示。 Engine是个抽象类,其主要的接口如下:
+ String[][] generateTestData(MetaParameter mp)
# String[][] generateRawTestData(MetaParameter mp)
generateTestData是供上层调用的公共方法,其在内部会调用generateRawTestData来产生原生的测试数据,并使用TestDataTransformer来转换原生的测试数据。MetaParameter包含了诸如因素、水平和强度等重要的输入信息。每个具体的Engine都要实现generateRawTestData这个抽象方法,以使用具体的策略来产生原生的测试数据。 AMEngine的内部设计如下图所示:
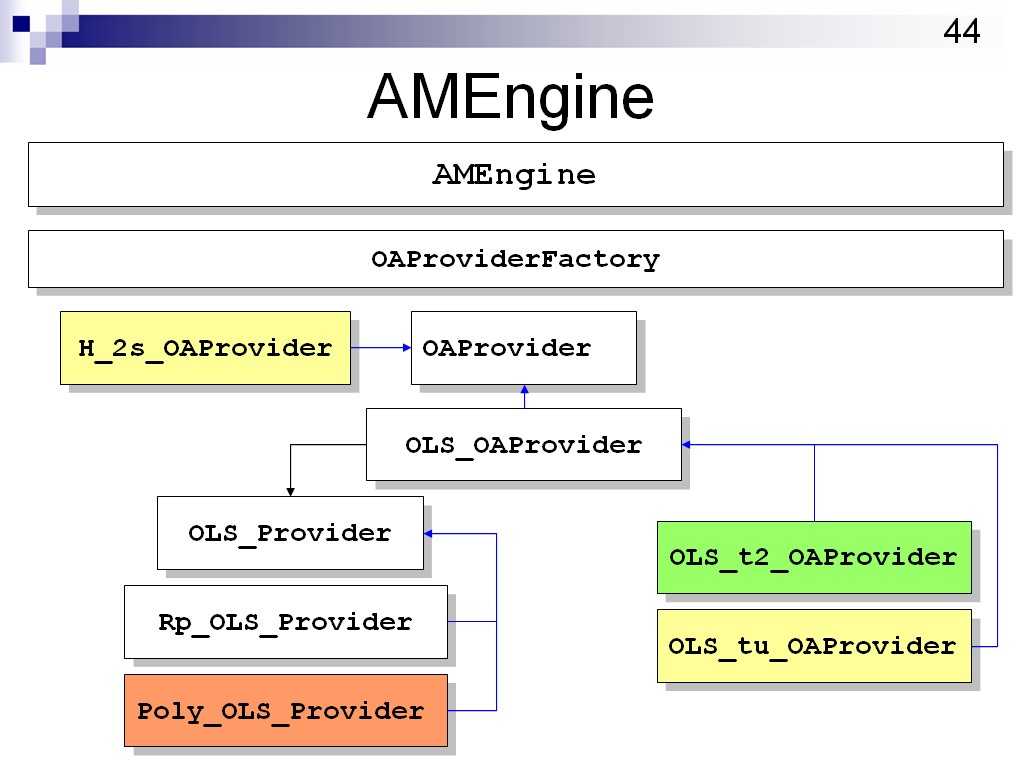
其中黑色箭头指代委托关系,蓝色线指代继承关系。 标绿色的OLS_t2_OAProvider是Lt2(tm)型正交表(t为素数或素数幂)的实现,其产生的正交表所对应的解是最优的。 H_2s_OAProvider是基于哈阵的直积来构造二水平正交表的实现,其产生的正交表所对应的解不全是最优的。 OLS_tu_OAProvider是为了解决因素数大于水平数加1情况时引入的一种解决方案,其产生的正交表所对应的解不是最优的。 OLS_OAProvider会委托OLS_Provider来产生正交拉丁方完全组,根据水平数为素数还是素数的方幂,决定使用基于以素数为模的剩余类域的Rp_OLS_Provider还是基于以不可约多项式为模的剩余类域的Poly_OLS_Provider。标红色的Poly_OLS_Provider的实现过程中使用了Jan Struyf所写的有限域的Java实现。 AMEngine在接收到上层系统的请求后,会委托OAProviderFactory来构造能处理该请求的OAProvider,如果无法处理则抛出异常。这样便把构造特定OAProvider的复杂逻辑从AMEngine分离出去,使职责得到分离,结构变得更清晰。
5.Pairwise Testing Service 适用情况
AMEngine在当各因素的水平数不同,或者因素数>水平数+1时,算法使用的是不完善的实现方法,当差距过大时不宜使用
还有一个问题是关于因素特定取值组合的非法性,比如IE浏览器与Solaris操作系统的配对是一种无效的组合,不应当在测试中出现。但是由于正交表的方式是一下子就构造出整个表来,而不像启发式算法是一条一条地生成测试用例来逐步满足Pairwise Testing所要求的测试覆盖。这个构造过程的区别决定了基于正交表的AMEngine不像其它基于启发式算法的Engine那样可以比较方便地处理该问题,当前的AMEngine实现并没有考虑这种情况的处理。
6.Pairwise Testing Service 性能对比
在一些特定的场合,具体来说就是当测试用例与正交表能完美结合,因素数<=水平数且各因素的水平数完全相同时,基于正交表的AMEngine在性能和质量上都远好于基于启发式算法的JennyEngine,但是由于数学性质的限制,能完全释放正交表威力的场合还是相对狭小,应用场合较少。
五、总结
最后回到Pairwise Testing的主题。其目的是为了提高软件测试的效率,那么Pairwise Testing是否就如80/20原则那样,只需花费很小的测试努力就能得到很大的测试回报?业界的应用给出了一些正面的例子,比如AT&T使用Pairwise Testing测试电子邮件软件StarMail,结果显示应用该方法后测试时间减少了一半,并且比传统测试方法多发现了28%的缺陷,生产率是原来的2.6倍。
Pairwise Testing的有效性正是因为它能检测出所有的单模和双模错误,并也能检测出很多多模错误,这与软件中的错误常常是由少数的几个变量相互作用引起的事实有着直接联系。但是也要警惕不要将Pairwise Testing看成是软件测试的银弹。挑选正确的因素需要花费精心的努力,需要领域专家、开发人员与测试人员的共同努力;并且决定各因素的水平值也需要结合已有的测试技术,如等价类划分和边界值分析等。应该结合使用多种测试技术才能在实际应用中取得较好的结果。并且在性命攸关的应用中Pairwise Testing的测试覆盖还达不到要求,需要应用强度大于2的组合测试或其它更严格的测试技术。
总之,Pairwise Testing不是万能的,需要挑选恰当的场合去应用,才能真正有效地提高测试的效率,改善软件的质量。
本文可理解为对Google Code 上 Pairwise Testing Service 的介绍,大量引述了其中的内容,若对作者的权益造成损害,请直接与我联系,我将无条件删除本文。
标签:
原文地址:http://www.cnblogs.com/yuexiaohao/p/4418013.html