标签：
本文是对 赵明老师 《计算机图形学》MOOC课程 部分章节的小总结。
直线是组成图形的基础，其算法往往被多次调用，其好坏直接影响图形的显示效果和速度。以下是一些画直线的常用算法。
1、DDA算法：
此算法基于增量思想。
对于直线的斜截式：y=kx+b，考虑每次 x 递增 1， 都有 y[i+1] = y[i] + k，这样就将 kx 部分的乘法转换成递推的加法。
由于像素点都是整数坐标，所以每次求得的 y 都要取整操作，采用加 0.5 取整数部分的方法：(int)(y[i]+0.5)。
但是，当 |k| > 1 时，由于 x 每次递增 1，会导致取的光栅采样点过稀，可能不足以近似趋近 理想的数学意义上的直线。
该算法的效率是：浮点数加法级别的。
2、中点画线法：
此算法依然基于增量思想。
对于直线的一般式：Ax+By+C=0，当|k|<1时，考虑每次 x 递增 1，y[i+1] 都只可能等于 y[i] 或者 y[i]+1，它取决于对于中点误差项的判断。
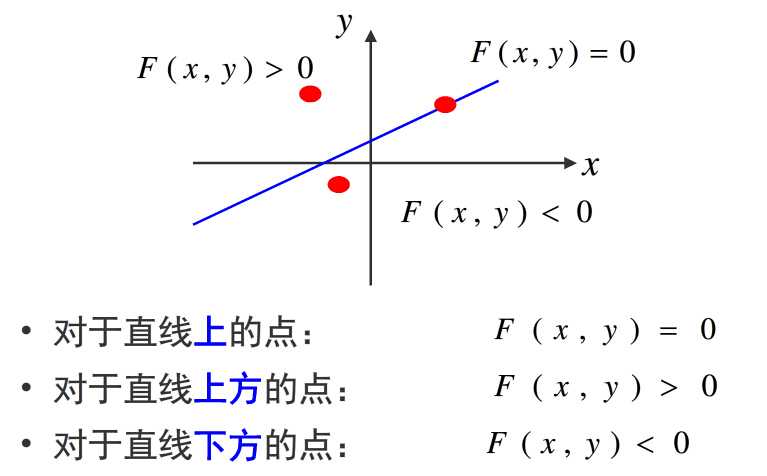
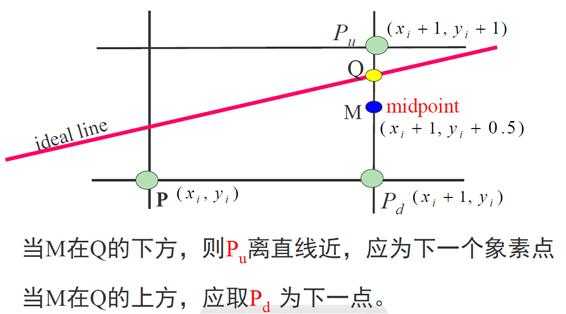
如何判断Q在M的上方还是下方？把 M 点代入直线一般式：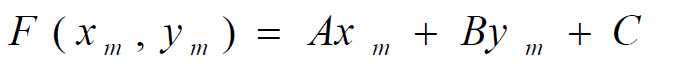
。
所以中点画线法的基本原理是：
接下来的关键在于推导出 d 的递推式以将乘法运算转换为加法运算。
当 d0<0，也就是取 Pu 时，对于下一个点：
；
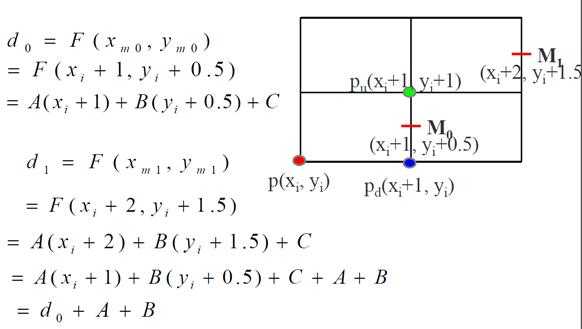当 d0>0，也就是取 Pd 时，对于下一个点：
。
（d只需要判断其符号，故可以用2d放大消除浮点运算）。
3、Bresenham 算法：
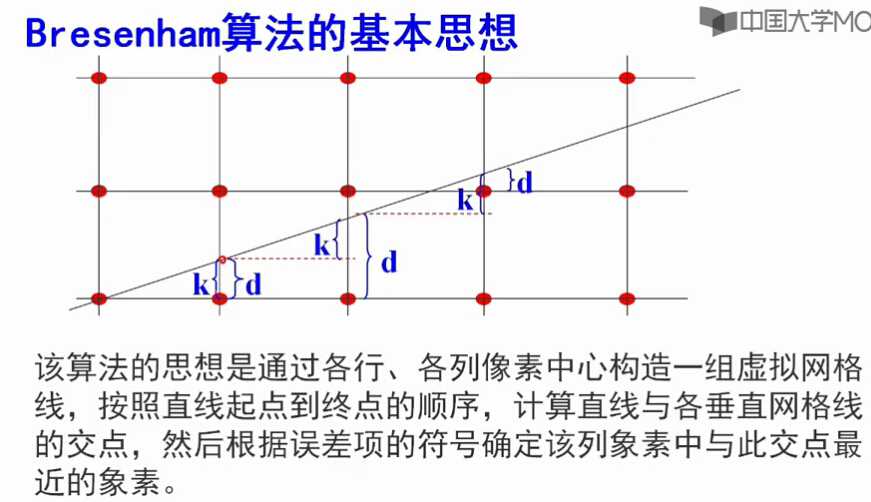
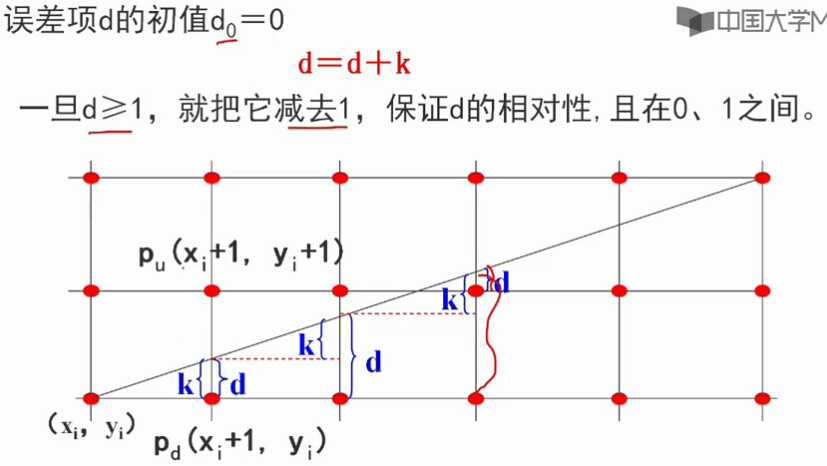
并且算法不依赖于直线方程的类型。
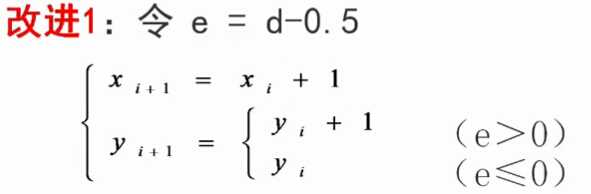
这样就将效率提高到了整数加法级别。
且不依赖于直线方程的形式。
标签：
原文地址：http://www.cnblogs.com/maples7/p/4419498.html
