标签:
结对成员:
朱少辉:主要负责代码编写
侯涛亮:主要负责程序测试
题目:一个首尾相接的一维整型数组,其中有正有负,求它的最大子数组并返回它的位置。
思路:在求一维子数组的基础上,先输入一个含有N个数的一维数组,将此数组向后平移N个使数组长度变为2N个,前N个和后N个值相等。再求这长度为2N的数组最大子数组之和,也就是求从第i个(i=0,1,2..n-1)到第i+n(不包含i+n)个中求最大的子数组和。这样会从0-N-1产生产生N个最大子数组的和,把这N个值存到另个数组中,求出最大值即为首位衔接一维子数组的最大值。该算法的时间复杂度为o(n^2)。
代码:
#include<iostream> #include<cmath> using namespace std; void main() { int a[25000],i,j,n,MaxSum,k,m,h,p; int f=0; int b[10],d[10]; cout<<"请输入数组中数字的个数"<<endl; cin>>n; cout<<"请输入数组"<<endl; for(i=0;i<n;i++) { cin>>a[i]; } for(i=n;i<2*n;i++) { a[i]=a[i-n]; } cout<<endl; for(i=0;i<n;i++) { k=0; MaxSum=0; h=i; for(j=i;j<i+n;j++) { k += a[j]; if(k > MaxSum) { MaxSum = k; h=j; } if(k < 0) { k = 0; } } d[i]=h; b[i]=MaxSum; } int c=b[0]; m=0; h=0; for(i=1;i<n;i++) { if(c<=b[i]) { c=b[i]; m=i; h=d[i]; } } p=h-n+1; if(p<=0) { p=n;} cout<<"从第"<<m+1<<"个到第"<<p<<"个"<<endl; cout<<"最大子数组为"<<endl; for(i=m;i<h+1;i++) { cout<<a[i]<<" ";} cout<<endl; cout<<"最大子数组之和为"<<c<<endl; }
截图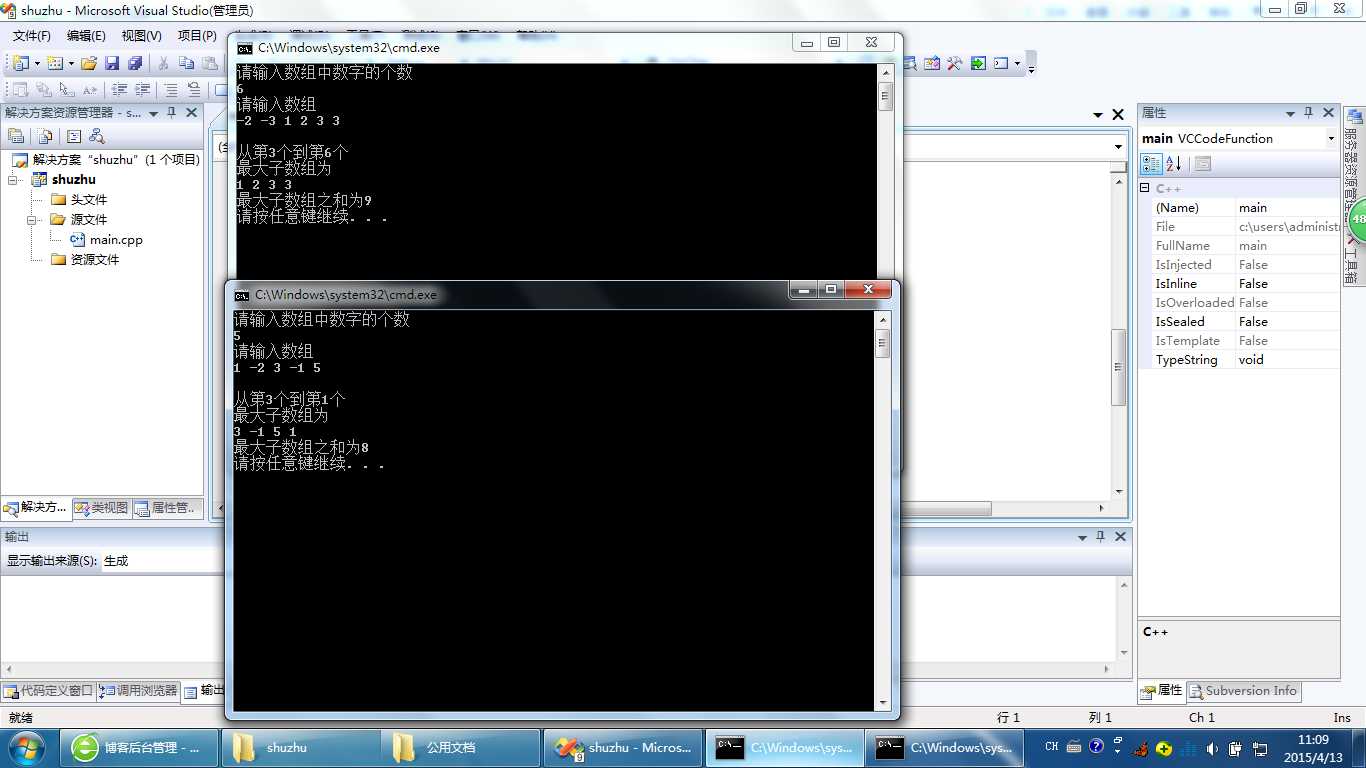
总结:
标签:
原文地址:http://www.cnblogs.com/bingoing/p/4421671.html