这个玩意代码量巨大,模仿着别人写了整整一天...
Java因为没有引用传递,所以构建树要么是全局设定根然后更改,要么函数返回的是根.....
红黑树确保没有一条路径比其他的路径长出2倍左右,因而是接近平衡的
1. 红黑树性质(限制):
1)每个结点要么是红的要么是黑的。
2)根结点是黑的。
3)每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。
4)如果一个结点是红的,那么它的两个儿子都是黑的。
5)对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。
2. 红黑树的性能分析:
挖坑,明天写.
3.预备知识:
左旋(右旋)指的是将这个点的右(左)子树占据自己的位置,原来的点变为其左(右)子树.
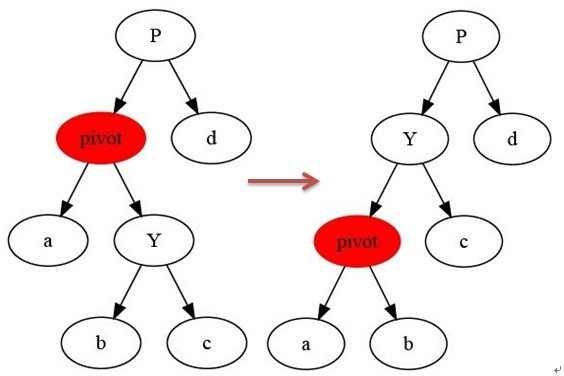
4.核心操作:
1) 插入
和AVL差不多,就是有个调整颜色的过程
/*
* 如果父节点是黑色就都没违反不用调整.
* 反之....
* 插入一个结点时。可能被破坏的性质为(4)如果一个结点是红色的,则它的孩子结点是黑色的 (2) 根结点是黑色的
* 插入修复情况1:如果当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色
* 插入修复情况2:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
* 插入修复情况3:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
*/2)删除
比较复杂,四种情况...
/* * 如果删除的是红色点,没影响........ * 如果删除的是黑色点,代替它位置的有红/黑两种情况, * 1. 红,直接将这个点改成黑色 * 2.1 黑且是根节点什么都不用做 * 2.2 删除修复情况1,当前节点颜色是黑,兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑) * 2.2删除修复情况2,当前节点颜色是黑,兄弟是黑色且兄弟节点的两个子节点全为黑色 * 2.2删除修复情况3,当前节点颜色是黑,兄弟节点是黑色,兄弟的左子是红色,右子是黑色 * 2.2删除修复情况4,当前节点颜色是黑,兄弟节点是黑色,但是兄弟节点的右子是红色, */
import java.util.Arrays;
import java.util.Collection;
import java.util.Scanner;
interface ANode{
public void rbInorderTravel(Node node);
public Node rbSearch(Node node);
public Node rbMinNode(Node node);
public Node rbMaxNode(Node node);
public boolean rbInsert(Node node,int data);
public boolean rbDelete(Node node,int data);
public void LL(Node node);
public void RR(Node node);
}
public class Main {
public static void main(String[] args) {
int [] a = new int[20];
for(int i = 0;i<20;i++){
a[i] = (int) (Math.random()*1000);
System.out.print(a[i] + " ");
Node.rbInsert(Node.root, a[i]);
}System.out.println();
Node.rbInorderTravel(Node.root);
Node.rbDelete(Node.root, a[1]);
Node.rbDelete(Node.root, a[9]);
Node.rbDelete(Node.root, a[0]);
Node.rbInorderTravel(Node.root);
}
}
class Node{
public static Node root = null;
public static int RED = 1;
public static int BLACK = 2;
Node lson,parent,rson;
int high;
int data;
int color;
public Node() {
super();
lson = rson = null;
high = 0;
this.color = RED;
}
public Node(int data) {
// TODO Auto-generated constructor stub
this();
this.data = data;
}
public void free(){
this.lson = this.rson = null;
this.parent = null;
}
public static Node rbSearch(Node node,int data){
while(node != null){
if(data < node.data)
node = node.lson;
else if(data > node.data)
node = node.rson;
else return node;
}
return null;
}
public static Node rbSuccessor(Node node){
Node pre = null;
while(node != null){
pre = node;
node = node.lson;
}
return pre;
}
public static void rbInorderTravel(Node node) {
// TODO Auto-generated method stub
if(null == node)
return;
rbInorderTravel(node.lson);
System.out.print(node.data+" ");
rbInorderTravel(node.rson);
if(node == root)
System.out.println();
}
public static boolean rbInsert(Node node, int data) {
// TODO Auto-generated method stub
Node now = new Node(data);
Node pre = null;
while(null != node){
pre = node;
if(data < node.data)
node = node.lson;
else node = node.rson;
}
if(pre == null)
root = now;
else{
if(data < pre.data)
pre.lson = now;
else pre.rson = now;
}
now.parent = pre;
rbTreeInsertFixup(now);
return true;
}
/*
* 如果父节点是黑色就都没违反不用调整.
* 反之....
* 插入一个结点时。可能被破坏的性质为(4)如果一个结点是红色的,则它的孩子结点是黑色的 (2) 根结点是黑色的
* 插入修复情况1:如果当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色
* 插入修复情况2:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
* 插入修复情况3:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
*/
private static void rbTreeInsertFixup(Node node) {
// TODO Auto-generated method stub
Node uncle,gparent,p;
while((p=node.parent) != null && p.color ==RED){
gparent = p.parent;
//如果父结点是祖父结点的左孩子(因为父结点是红色结点,所以肯定有祖父结点)
if(p == gparent.lson){
uncle = gparent.rson;
if(uncle != null && uncle.color == RED){//修复情况1
gparent.color = RED;
p.color = BLACK;
uncle.color = BLACK;
node = gparent;
}else{ //叔父不存在或者存在但是颜色是黑色的,则必须通过寻转来配合改变颜色来保持性质2
if(node == p.rson){//修复情况2
node = p;
LL(node);
p = node.parent;
}// 情况2:x为其父结点的右孩子,通过左旋转换为情况3
//情况三:x为其父结点的左孩子,调整父结点和祖父结点的颜色,以纠正性质4,但是破坏了性质5
p.color = BLACK;
gparent.color = RED;
RR(gparent);//此时x->parent->color = BLACK, 循环结束
}
}else{
uncle = gparent.lson;
if(uncle != null && uncle.color == RED){
gparent.color = RED;
p.color = BLACK;
uncle.color = BLACK;
node = gparent;
}else{ //叔父不存在或者存在但是颜色是黑色的,则必须通过寻转来配合改变颜色来保持性质2
if(node == p.lson){
node = p;
RR(node);
p = node.parent;
}// 情况2:x为其父结点的右孩子,通过左旋转换为情况3
//情况三:x为其父结点的左孩子,调整父结点和祖父结点的颜色,以纠正性质4,但是破坏了性质5
p.color = BLACK;
gparent.color = RED;
LL(gparent);//此时x->parent->color = BLACK, 循环结束
}
}
}
root.color = BLACK;//保持性质2,根为黑色
}
/*
* 如果删除的是红色点,没影响........
* 如果删除的是黑色点,代替它位置的有红/黑两种情况,
* 1. 红,直接将这个点改成黑色
* 2.1 黑且是根节点什么都不用做
* 2.2 删除修复情况1,当前节点颜色是黑,兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑)
* 2.2删除修复情况2,当前节点颜色是黑,兄弟是黑色且兄弟节点的两个子节点全为黑色
* 2.2删除修复情况3,当前节点颜色是黑,兄弟节点是黑色,兄弟的左子是红色,右子是黑色
* 2.2删除修复情况4,当前节点颜色是黑,兄弟节点是黑色,但是兄弟节点的右子是红色,
*
* 另一种解释:
* 删除一个黑结点会导致如下三个问题:
* (1)如果被删除结点y是根结点,而y的一个红色孩子成为了新的根,则违反了性质2
* (2)如何y的父结点和其孩子结点都是红色的,则违反了性质4
* (3)删除y将导致先前包含y的任何路径上的黑结点树少一个,破坏了性质5。
* 解决方案是:被删除的结点黑色属性下移到其孩子结点x上。此时性质5都得以保持,于是存在2种情况:
* (1)x原来为红色,此时孩子结点属性是红黑,此时破坏了性质(1),(4),如果x还是树根则,破坏了性质(2)
* 处理方式为:将x重新着色为黑色(此操作同时去除其多余的黑色属性),处理完毕,红黑树性质得以保持
* (2)x原来为黑色,此时x的属性为双重黑色,破坏了性质(1),若x为树根,则可以只是简单的消除x多余的黑色属性
* 否则需要做必要的旋转和颜色修改
*/
public static boolean rbDelete(Node node, int data) {
// TODO Auto-generated method stub
Node now = rbSearch(node,data);
Node pre = now;
Node son = null;
if(now == null)
return false;
if(now.lson != null && now.rson != null){
now = rbSuccessor(now.rson);
pre.data = now.data;
}else if(now.lson != null)
son = now.lson;
else if(now.rson != null)
son = now.rson;
if(son != null)
son.parent = now.parent;
if(now.parent == null)
root = son;
else{
if(now.parent.lson == now)
now.parent.lson = son;
else now.parent.rson = son;
}
if(now.color == BLACK)
rbTreeDeleteFixup(root,now.parent,son);
now.free();
return true;
}
private static void rbTreeDeleteFixup(Node root,Node parent, Node node) {
// TODO Auto-generated method stub
Node brother = null;
while( ( node==null || node.color==BLACK ) && node != root){
if(node == parent.lson){
brother = parent.rson;
//情况1:如果兄弟结点为红色,则parent颜色比为黑色,此时调整颜色,并左旋,使得brother和
//parent位置调换,此操作不破坏别的性质,并将情况1变化为情况2,3,4
if(brother.color == RED){
parent.color = RED;
brother.color = BLACK;
LL(parent);
brother = parent.rson;
}
//情况2,这里没有加brother==black是因为经过情况1定然满足
//brother有两个黑色结点(NULL也为黑色结点):将x和brother抹除一重黑色
//具体操作为,brother的颜色变为红,x结点上移到其父结点
if((brother.lson == null || brother.lson.color == BLACK) &&
(brother.rson == null || brother.rson.color == BLACK)){
brother.color = RED;
node = parent;
parent = parent.parent;
}else{
//从上面的if中已经知道两个孩子不都是黑色
//情况3: brother左孩子为红色结点,右孩子为黑色结点
if(brother.rson == null || brother.rson.color == BLACK){
brother.lson.color = BLACK;
brother.color = RED;
RR(brother);//右旋使情况3变化为情况4
brother = parent.rson;//因为旋转,重置
}
//情况4:brother的右孩子为红色结点:
//交换brother和parent的颜色和位置,使得x的2重黑色属性中的一重转移到其parent上
//此时到brother的右孩子的黑结点数少一,于是将右结点的颜色置黑,红黑树性质得以保持
brother.color = parent.color;
parent.color = BLACK;
brother.rson.color = BLACK;
LL(parent);
node = root;
}
}else{
brother = parent.lson;
//情况1:如果兄弟结点为红色,则parent颜色比为黑色,此时调整颜色,并左旋,使得brother和
//parent位置调换,此操作不破坏别的性质,并将情况1变化为情况2,3,4
if(brother.color == RED){
parent.color = RED;
brother.color = BLACK;
RR(parent);
brother = parent.lson;
}
//情况2,这里没有加brother==black是因为经过情况1定然满足
//brother有两个黑色结点(NULL也为黑色结点):将x和brother抹除一重黑色
//具体操作为,brother的颜色变为红,x结点上移到其父结点
if((brother.lson == null || brother.lson.color == BLACK) &&
(brother.rson == null || brother.rson.color == BLACK)){
brother.color = RED;
node = parent;
parent = parent.parent;
}else{
//从上面的if中已经知道两个孩子不都是黑色
//情况3: brother右孩子为红色结点,左孩子为黑色结点
if(brother.lson == null || brother.lson.color == BLACK){
brother.rson.color = BLACK;
brother.color = RED;
LL(brother);//右旋使情况3变化为情况4
brother = parent.rson;//因为旋转,重置
}
//情况4:brother的右孩子为红色结点:
//交换brother和parent的颜色和位置,使得x的2重黑色属性中的一重转移到其parent上
//此时到brother的右孩子的黑结点数少一,于是将右结点的颜色置黑,红黑树性质得以保持
brother.color = parent.color;
parent.color = BLACK;
brother.lson.color = BLACK;
RR(parent);
node = root;
}
}
}
if(node != null)
node.color = BLACK;
}
/**
* 红黑树的左转与AVL的不同,LL是root.left.right提上去
* @param node
*/
public static void LL(Node node) {
// TODO Auto-generated method stub
Node son = node.rson;
node.rson = son.lson;
if(son.lson != null)
son.lson.parent = node;
son.parent = node.parent;
//node 为树根
if(node.parent == null)
root = son;
else{
if(node.parent.lson == node)
node.parent.lson = son;
else node.parent.rson = son;
}
son.lson = node;
node.parent = son;
}
public static void RR(Node node) {
// TODO Auto-generated method stub
Node son = node.lson;
node.lson = son.rson;
if(son.rson != null)
son.rson.parent = node;
son.parent = node.parent;
//node 为树根
if(node.parent == null)
root = son;
else{
if(node.parent.lson == node)
node.parent.lson = son;
else node.parent.rson = son;
}//要修改parent,parent的左右,本身指针
son.rson = node;
node.parent = son;
}
}
原文地址:http://blog.csdn.net/gg_gogoing/article/details/45039115