标签:
浅谈拓扑排序在OI的应用
by MedalPluS
【拓扑排序的定义】
引例:
在大学里有很多学科需要学习,而有的学科需要学习其他学科后才能学习,比如说必须先学数学再学微积分......这就是一个拓扑序的关系
【拓扑排序的应用】
对于上述题目,可以假设如果学习a需要学习b的话,从b连一条边到a,然后对整个图求一次拓扑序列,这便是学习的一种方案
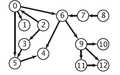
很显然,拓扑排序应该从入度为0,然后1,然后2...来找
【拓扑排序的实现】
很容易想到一种算法,暴力枚举每个点,然后找与之相连的点,删掉这条边,并把点的入度-1,再次寻找,知道找不到为止
裸的算法为O(n2)
我们发现,拓扑排序的结果是拓扑序,那么可以用队列来改造,而枚举边又耗时,所以就用邻接表来存储
时间复杂度O(n+e)
【拓扑排序在OI的应用】
例题1.郁闷的记者
【问题描述】
你是一个体育报社的记者,你接受到一项艰难的任务:有N支足球队参加足球比赛,现在给你一些比赛的结果,需要你给你各支球队的排名,从1到N。
以下是给你的一些信息:
(1)没有平局;
(2)不同的球队排名不能相同;
(3)对于所有满足1≤a<b≤N,第a名的球队一定可以打败第b名的球队。
给你部分比赛结果,要求给出排名。
【输入格式】
第一行输入N(1≤N≤5000),表示球队的数量,编号为1到N。
第二行输入M(1≤M≤100000),表示给出的比赛场数。接下来M行,每行两个整数xi,yi,表示球队xi能打败球队yi。
【输出格式】
输出包含N行,前N行描述球队的排名,第i个数表示排名为i的球队编号。
【分析】
我们可以建立一个模型,假设每个球队是一个点,那么如果a能打败b则从a到b连一条有向边。
由于求排名,很明显,入度为0的第一,其次第二,第三....
发现没?这便是拓扑排序的模板!
我们使用o(N+e)的代码,见附录1
例题2.奇怪的梦境
题目描述 Description
Aiden陷入了一个奇怪的梦境:他被困在一个小房子中,墙上有很多按钮,还有一个屏幕,上面显示了一些信息。屏幕上说,要将所有按钮都按下才能出去,而又给出了一些信息,说明了某个按钮只能在另一个按钮按下之后才能按下,而没有被提及的按钮则可以在任何时候按下。可是Aiden发现屏幕上所给信息似乎有矛盾,请你来帮忙判断。
输入描述 Input Description
第一行,两个数N,M,表示有编号为1...N这N个按钮,屏幕上有M条信息。
接下来的M行,每行两个数ai,bi,表示bi按钮要在ai之后按下。所给信息可能有重复,保证ai≠bi。
输出描述 Output Description
若按钮能全部按下,则输出“o(∩_∩)o”。
若不能,第一行输出“T_T”,第二行输出因信息有矛盾而无法确认按下顺序的按钮的个数。输出不包括引号。
样例输入 Sample Input
3 3
1 2
2 3
3 2
样例输出 Sample Output
T_T
2
数据范围及提示 Data Size & Hint
对于30%的数据,保证0<N≤100。
对于50%的数据,保证0<N≤2000。
对于70%的数据,保证0<N≤5000。
对于100%的数据,保证0<N≤10000,0<M≤2.5N。
【分析】
首先,不难发现题目是求拓扑排序(0.0),把每个按钮抽象1成点,a在b之前则从a连一条到b的边,然后求拓扑排序,统计有多少个点没有被扫到
时间复杂度O(n+m),不会TLE
代码见附录2
【总结】
附录1.
1 #include <iostream> 2 #include <cstdio> 3 #include <queue> 4 using namespace std; 5 6 const int maxn=5001; 7 const int maxm=1000001; 8 9 int in[maxn]; 10 int n,m,u,v; 11 12 struct edge{ 13 int next,to; 14 }g[maxm]; 15 16 int head[maxn],cnt; 17 18 void addedge(int u,int v){ 19 cnt++; 20 g[cnt].to=v; 21 g[cnt].next=head[u]; 22 head[u]=cnt; 23 } 24 25 queue<int> q; 26 void top_sort(){ 27 int u,i,j; 28 for(i=1;i<=n;i++) 29 if(!in[i])q.push(i); 30 while(!q.empty()){ 31 u=q.front(); 32 cout<<u<<endl; 33 q.pop(); 34 for(j=head[u];j;j=g[j].next) 35 { 36 in[g[j].to]--; 37 if(in[g[j].to]==0) 38 q.push(g[j].to); 39 } 40 } 41 } 42 43 int main(){ 44 freopen("rank.in","r",stdin); 45 freopen("rank.out","w",stdout); 46 cin>>n>>m; 47 int i; 48 for(i=1;i<=m;i++){ 49 scanf("%d%d",&u,&v); 50 addedge(u,v); 51 in[v]++; 52 } 53 top_sort(); 54 return 0; 55 }
附录2.
#include <iostream> #include <cstdio> #include <queue> using namespace std; const int maxn=25005; struct edge{ int next,to; }g[maxn]; int head[maxn],cnt; int n,m,in[maxn]; int inq; void addedge(int u,int v){ cnt++; g[cnt].to=v; g[cnt].next=head[u]; head[u]=cnt; } void topsort(){ queue<int> q; int i,ahead; for(i=1;i<=n;i++) if(!in[i]) q.push(i); while(!q.empty()){ ahead=q.front(); q.pop(); inq++; for(i=head[ahead];i;i=g[i].next) { in[g[i].to]--; if(in[g[i].to]==0)q.push(g[i].to); } } if(inq==n)cout<<"O(∩_∩)O"; else cout<<"T_T"<<endl<<n-inq; } int main(){ cin>>n>>m; int u,v; for(int i=1;i<=m;i++){ scanf("%d%d",&u,&v); addedge(u,v); in[v]++; } topsort(); return 0; }
标签:
原文地址:http://www.cnblogs.com/maopengsen/p/4433373.html