标签:
Random类 (java.util)
Random类中实现的随机算法是伪随机,也就是有规则的随机。在进行随机时,随机算法的起源数字称为种子数(seed),在种子数的基础上进行一定的变换,从而产生需要的随机数字。
相同种子数的Random对象,相同次数生成的随机数字是完全相同的。也就是说,两个种子数相同的Random对象,第一次生成的随机数字完全相同,第二次生成的随机数字也完全相同。这点在生成多个随机数字时需要特别注意。
下面介绍一下Random类的使用,以及如何生成指定区间的随机数组以及实现程序中要求的几率。
1、Random对象的生成
Random类包含两个构造方法,下面依次进行介绍:
a、public Random()
该构造方法使用一个和当前系统时间对应的相对时间有关的数字作为种子数,然后使用这个种子数构造Random对象。
b、public Random(long seed)
该构造方法可以通过制定一个种子数进行创建。
示例代码:
Random r = new Random();
Random r1 = new Random(10);
再次强调:种子数只是随机算法的起源数字,和生成的随机数字的区间无关。
验证:相同种子数的Random对象,相同次数生成的随机数字是完全相同的。
import java.util.Random;
public class test {
public void random(){
int i=0;
int j=0;
Random random=new Random(1);
Random random1=new Random(1);
i=random.nextInt();
j=random1.nextInt();
System.out.println(i+"-----"+j);
}
public static void main(String[] args) {
test tt=new test();
tt.random();
}
}
结果:
第一次:

修改一下起源数字,让其等于10。
Random random=new Random(10);
Random random1=new Random(10);
观察结果:
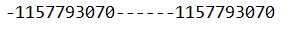
2、Random类中的常用方法
Random类中的方法比较简单,每个方法的功能也很容易理解。需要说明的是,Random类中各方法生成的随机数字都是均匀分布的,也就是说区间内部的数字生成的几率是均等的。下面对这些方法做一下基本的介绍:
a、public boolean nextBoolean():是生成一个随机的boolean值,生成true和false的值几率相等,也就是都是50%的几率。
b、public double nextDouble():是生成一个随机的double值,数值介于[0,1.0)之间。
c、public int nextInt():是生成在-2^31到2^31-1之间int值。如果需要生成指定区间的int值,则需要进行一定的数学变换,具体可以参看下面的使用示例中的代码。
d、public int nextInt(int n):是生成一个介于[0,n)的区间int值,包含0而不包含n。如果想生成指定区间int值,也需要进行一定的数学变换,具体参看下面的使用示例中的代码。
e、public void setSeed(long seed):是重新设置Random对象中的种子数。设置完种子数以后的Random对象和相同种子数使用new关键字创建出的Random对象相同。
f、 public float nextFloat(int n):返回下一个伪随机数,它是取自此随机数生成器序列的、在 0.0 和 1.0 之间均匀分布的 float 值。
g、 public long nextLong():返回下一个伪随机数,它是取自此随机数生成器序列的均匀分布的 long 值。
h、public double nextGaussian():返回下一个伪随机数,它是取自此随机数生成器序列的、呈高斯(“正态”)分布的 double 值,其平均值是 0.0,标准差是 1.0。
3、Random类使用示例
使用Random类,一般是生成指定区间的随机数字,下面就一一介绍如何生成对应区间的随机数字。以下生成随机数的代码均使用以下Random对象r进行生成:
Random r = new Random();
a、生成[0,1.0)区间的小数
double d1 = r.nextDouble();//直接使用nextDouble方法获得。
b、生成[0,5.0)区间的小数
double d2 = r.nextDouble() * 5;//因为扩大5倍即是要求的区间。同理,生成[0,d)区间的随机小数,d为任意正的小数,则只需要将nextDouble方法的返回值乘以d即可。
c、生成[1,2.5)区间的小数
double d3 = r.nextDouble() * 1.5 + 1;//生成[1,2.5)区间的随机小数,则只需要首先生成[0,1.5)区间的随机数字,然后将生成的随机数区间加1即可。
同理,生成任意非从0开始的小数区间[d1,d2)范围的随机数字(其中d1不等于0),则只需要首先生成[0,d2-d1)区间的随机数字,然后将生成的随机数字区间加上d1即可。
d、生成任意整数(-2^31到2^31-1之间)
int n1 = r.nextInt();//直接使用nextInt方法即可。
e、生成[0,10)区间的整数
int n2 = r.nextInt(10);
n2 = Math.abs(r.nextInt() % 10);
以上两行代码均可生成[0,10)区间的整数。
第一种实现使用Random类中的nextInt(int n)方法直接实现。
第二种实现中,首先调用nextInt()方法生成一个任意的int数字,该数字和10取余以后生成的数字区间为(-10,10),然后再对该区间求绝对值,则得到的区间就是[0,10)了。
同理,生成任意[0,n)区间的随机整数,都可以使用如下代码:
int n2 = r.nextInt(n);
n2 = Math.abs(r.nextInt() % n);
f、生成[0,10]区间的整数
int n3 = r.nextInt(11);
n3 = Math.abs(r.nextInt() % 11);
相对于整数区间,[0,10]区间和[0,11)区间等价,所以即生成[0,11)区间的整数。
g、生成[-3,15)区间的整数
int n4 = r.nextInt(18) - 3;
n4 = Math.abs(r.nextInt() % 18) - 3;
生成非从0开始区间的随机整数,可以参看上面非从0开始的小数区间实现原理的说明。
h、几率实现
按照一定的几率实现程序逻辑也是随机处理可以解决的一个问题。下面以一个简单的示例演示如何使用随机数字实现几率的逻辑。
在前面的方法介绍中,nextInt(int n)方法中生成的数字是均匀的,也就是说该区间内部的每个数字生成的几率是相同的。那么如果生成一个[0,100)区间的随机整数,则每个数字生成的几率应该是相同的,而且由于该区间中总计有100个整数,所以每个数字的几率都是1%。按照这个理论,可以实现程序中的几率问题。
示例:随机生成一个整数,该整数以55%的几率生成1,以40%的几率生成2,以5%的几率生成3。实现的代码如下:
int n5 = r.nextInt(100);
int m; //结果数字
if(n5 < 55){ //55个数字的区间,55%的几率
m = 1;
}else if(n5 < 95){//[55,95),40个数字的区间,40%的几率
m = 2;
}else{
m = 3;
}
因为每个数字的几率都是1%,则任意55个数字的区间的几率就是55%,为了代码方便书写,这里使用[0,55)区间的所有整数,后续的原理一样。
当然,这里的代码可以简化,因为几率都是5%的倍数,所以只要以5%为基础来控制几率即可,下面是简化的代码实现:
int n6 = r.nextInt(20);
int m1;
if(n6 < 11){
m1 = 1;
}else if(n6 < 19){
m1= 2;
}else{
m1 = 3;
}
在程序内部,几率的逻辑就可以按照上面的说明进行实现。
4、其它问题
a、相同种子数Random对象问题
前面介绍过,相同种子数的Random对象,相同次数生成的随机数字是完全相同的,下面是测试的代码:
Random r1 = new Random(10);
Random r2 = new Random(10);
for(int i = 0;i < 2;i++){
System.out.println(r1.nextInt());
System.out.println(r2.nextInt());
}
在该代码中,对象r1和r2使用的种子数都是10,则这两个对象相同次数生成的随机数是完全相同的。
如果想避免出现随机数字相同的情况,则需要注意,无论项目中需要生成多少个随机数字,都只使用一个Random对象即可。
b、关于Math类中的random方法
其实在Math类中也有一个random方法,该random方法的工作是生成一个[0,1.0)区间的随机小数。
通过阅读Math类的源代码可以发现,Math类中的random方法就是直接调用Random类中的nextDouble方法实现的。
只是random方法的调用比较简单,所以很多程序员都习惯使用Math类的random方法来生成随机数字。
标签:
原文地址:http://www.cnblogs.com/weink1215/p/4433790.html