标签:
堆排序,顾名思义利用堆的性质进行排序。堆都有哪些性质,比如:一堆沙子、一堆泥土
二叉堆实际上是一课完全二叉树,同时满足:父结点的键值总是大于或等于(小于或等于)任何一个子结点的键值
当父结点的键值总是大于或等于任何一个子结点的键值时称为 最大堆
当父结点的键值总是小于或等于任何一个子结点的键值时称为 最小堆
二叉堆又简称为 堆,通常用数组来实现
i 结点的父结点的下标是: (i-1) / 2 , 左子树的下标是:2 * i + 1 , 又子树的下标是: 2 * i + 2
堆排序中首先需要解决的问题是将数组进行堆化(下面以最小堆为例)
给定数组 a[] = {9,12,17,30,50,20,60,65,4,19} ;
初始化堆如下图:
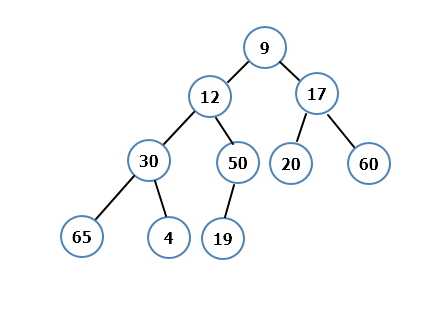
对数组进行堆化后如下图:
#include<stdio.h> void makeMinHead(int a[] , int n) { for(int i = n / 2 - 1 ; i >= 0 ; i--) { int k = i ; int temp = a[k] ; for(int j = 2 * k + 1 ; j < n ; ) { if(j + 1 < n && a[j+1] < a[j]) j++ ; if(temp <= a[j]) break ; a[k] = a[j] ; k = j ; j = 2 * k + 1 ; } a[k] = temp ; } } int main() { int a[] = {9,12,17,30,50,20,60,65,4,19} ; makeMinHead(a,10) ; for(int i = 0 ; i < 10 ; i++) printf("%d ",a[i]) ; printf("\n") ; return 0 ; }
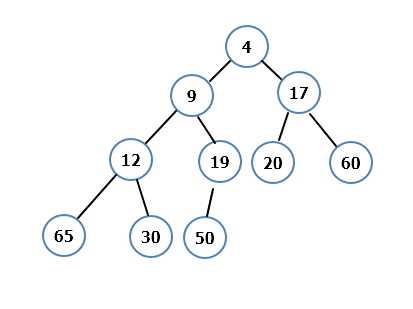
堆化数组之后,第0个数据是堆中最小的数据,删除第0个元素,同时把最后一个元素放到第0个元素的位置上,不断缩小堆中元素,则第一小,第二小,第三小……分别被查找出来,堆排序结束;
具体过程如下:
#include<stdio.h> void makeMinHead(int a[] , int n) { for(int i = n / 2 - 1 ; i >= 0 ; i--) { // 对数组进行堆化 int k = i ; // 从第一个非叶子结点开始 int temp = a[k] ; for(int j = 2 * k + 1 ; j < n ; ) { // 和插入排序类似 if(j + 1 < n && a[j+1] < a[j]) // 左子树和右子树中取最小值 j++ ; if(temp <= a[j]) // 如果父结点的键值小于或等于两个儿子结点中的最小值,这不再需要调整 break ; a[k] = a[j] ; // 如果父结点的键值大于两个儿子结点中的最小值,继续交换 k = j ; j = 2 * k + 1 ; } a[k] = temp ; } } void Swap(int &a , int &b) { a = a ^ b ; b = a ^ b ; a = a ^ b ; } void HeadSort(int a[] , int n) { // 堆排序过程 for(int i = n-1 ; i > 0 ; i--) { // 每调整一次,找出一个最小值 int temp = a[0] ; // 将第0个数据放到合适的位置上 int k = 0 ; for(int j = 2 * k + 1 ; j <= i ;) { if(j + 1 <= i && a[j + 1] < a[j]) j++ ; if(temp <= a[j]) break ; a[k] = a[j] ; k = j ; j = 2 * k + 1 ; } a[k] = temp ; Swap(a[0] , a[i]) ; // 将最小值放到数组后边 } } int main() { int a[] = {9,12,17,30,50,20,60,65,4,19} ; makeMinHead(a,10) ; Swap(a[0],a[9]) ; HeadSort(a,9) ; for(int i = 9 ; i >= 0 ; i--) printf("%d ",a[i]) ; printf("\n") ; return 0 ; }
标签:
原文地址:http://www.cnblogs.com/scottdinggo/p/4437640.html