标签:
RSA算法 是一种公钥加密算法,RSA算法相比别的算法思路非常清晰,但是想要破解的难度非常大。RSA算法基于一个非常简单的数论事实:两个素数相乘得到一个大数很容易,但是由一个大数分解为两个素数相乘却非常难。这种算法是在1978年首次亮相,它是第一个既能用于数据加密也可以用于数字签名的算法,而且理解起来简单容易。早在1973,就有密码学家发现了类似的算法,但是一直被列为绝密直到1998年才被正式公开出来。
RSA算法是一种非对称的算法,该算法需要一对密钥使用其中一个加密另一个就可以进行解密。首先我们来认识一下欧拉函数:
欧拉函数的通式形如:φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn),计算出来的值是小于x的自然数中素数的个数,关于正确性数论上有严格的证明。
在RSA算法中我们的初始的两个素数是p和q,而欧拉函数的参数x就是p*q,那么欧拉函数就可以变形为:φ(p*q)=(p-1)*(q-1)
然后我们需要以下两个步骤来计算出一对可以用来进行加密和解密的密钥:
(1)找到任意一个数d,使得d和p*q互质,即gcd(d,p*q)=1(最大公约数 of greatest common divisor)
(2)计算出一个e,满足gcd(d*e,p*q)=1
比如举p=3,q=7为例子,那么假设使d=5满足gcd(21,5)=1,那么对应的e就应该满足gcd(5*e,21)=1,得e=17,这样一来我们就得到了一对公钥和密钥d,e。
假设要加密数据3,那么就有(3)^d mod p*q=243mod21=12 所以加密之后我们得到的数据就是12
对于解密过程,我们对加密后的数据 (12)^e mod p*q=12^17mod21=(12^5)mod21 * (12^5)mod 21 * (12^5)mod21 * (12)^2mod21=((7^3)mod21)*3mod21=3
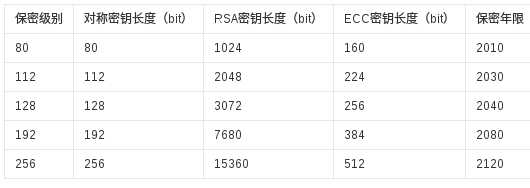
整个RSA加密解密算法的过程简单的有些令人担忧他的安全性,但是上图给了我们一个肯定的答复,随着RSA密钥长度的增加,保密的年限会加速增长,在当今现代如果不考虑量子计算机暴力破解的话,RSA算法的加密的安全是可以保证的,除非数学界会有发现新的方法可以快速算出一个大数(可以非常大)分为两个质数的乘积的算法。
有了以上的基础我们就可以对长的数据进行分组从而完成加密处理:
1 #include<stdio.h> 2 #include<stdlib.h> 3 4 5 #define KEY_LEN_LIMIT 1024 6 7 #define TRUE 1 8 #define FALSE 0 9 10 unsigned prime1,prime2; 11 char buf[KEY_LEN_LIMIT]={}; 12 unsigned pub,sec=2; 13 14 15 void swap(unsigned*l,unsigned*r){ 16 unsigned tmp=*l; 17 *l=*r; 18 *r=tmp; 19 } 20 21 unsigned gcd(unsigned a,unsigned b){ 22 if(a<b)swap(&a,&b); 23 if(b==0)return a; 24 else return gcd(b,a%b); 25 } 26 27 28 void encrypt(char*p,unsigned key,unsigned mod){ 29 char tmp=*p; 30 for(unsigned i=2;i<=key;i++){ 31 tmp=(tmp*tmp)%mod; 32 } 33 *p=tmp; 34 } 35 36 void decrypt(char*p,unsigned key,unsigned mod){ 37 char tmp=*p; 38 for(unsigned i=2;i<=key;i++){ 39 tmp=(tmp*tmp)%mod; 40 } 41 *p=tmp; 42 } 43 44 int main(int argc,char*argv[]){ 45 printf("Input Your Primary Letter/Number 1st to Generate Key:"); 46 scanf("%u",&prime1); 47 printf("Input Your Primary Letter/Number 2nd to Generate Key:"); 48 scanf("%u",&prime2); 49 unsigned tmp1=(unsigned)prime1,tmp2=(unsigned)prime2; 50 unsigned mul=(tmp1-1)*(tmp2-1); 51 printf("Input Your 1st Public Key:"); 52 scanf("%u",&pub); 53 while(gcd(pub,mul)!=1){ 54 printf("Input Your 1st Public Key:(Illegal)"); 55 scanf("%u",&pub); 56 } 57 printf("Now The Secret Key is:"); 58 while(((pub*sec)%mul)!=1)sec++; 59 printf("%u\n",sec); 60 printf("Finally Input Your Plain Text to Encrypt:"); 61 scanf("%s",buf); 62 printf("The Encrypted Text is:"); 63 for(int i=0;i<KEY_LEN_LIMIT;i++){ 64 if(buf[i]==0)break; 65 else{ 66 encrypt(&buf[i],pub,mul); 67 printf("%u",buf[i]); 68 } 69 }putchar(‘\n‘); 70 printf("The Decrypted Text is:"); 71 for(int i=0;i<KEY_LEN_LIMIT;i++){ 72 if(buf[i]==0)break; 73 else{ 74 decrypt(&buf[i],sec,mul); 75 printf("%c",buf[i]); 76 } 77 }putchar(‘\n‘); 78 return 0; 79 }
标签:
原文地址:http://www.cnblogs.com/guguli/p/4442761.html