标签:

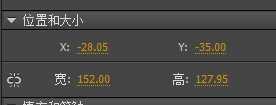
如上图所示,这样的一个简单矩形,边界矩形是(x:-28, y:-35, width:152, height:128),这是在这个元件/显示对象自己的坐标空间的范围。
那么把这个放到父元件(舞台)中,再做一定变换。如下图所示,白色区域就是舞台,蓝色矩形中的白色十字架标记,就是世界坐标的(0,0)点。

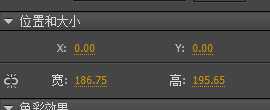
在舞台这个世界坐标系中,边界区域又是什么呢?我们的目标就是计算下图中的红色区域。

其实算法,很简单,在放到舞台之前,在蓝色矩形自己的局部坐标系中,边界是(x:-28, y:-35, width:152, height:128)。
那么,4个顶点坐标是可以轻易找到的:(-28,-35)、(152-28,-35)、(152,128)、(-28,128-35)。
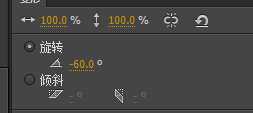
矩形旋转了-60度,其实这个变换,可以具体转化为一个Matrix矩阵变换。通过自己计算或者利用Flash等辅助,可以知道Matrix如下:
Matrix (a=0.4999847412109375, b=-0.865966796875, c=0.86602783203125, d=0.500030517578125, tx=-44.3, ty=6.8)
最后,计算出每个顶点经过Matrix变换后的新坐标,再通过这4个新坐标,算出上下左右的边框位置。
什么?怎么计算这个Matrix?好吧,先插播一下Matrix的计算。
首先,当然你得有一个Matrix类,可以参考任意语言的Matrix2D,其实都一样的。abcd和tx、ty,6个属性。
然后Matrix中实现rotate、translate等方法。
最后,简单2句,就可以算出:
var matrix = new Matrix2D(); matrix.rotate(-60*Math.PI/180);
回到正题,先把Matrix和rect的计算,封装一下:
p._transformBounds = function (bounds, matrix) { if(bounds.x || bounds.y){ matrix.append(1,0,0,1,bounds.x,bounds.y); } var lt = {x:0, y:0}; var rt = {x:bounds.width, y:0}; var lb = {x:0, y:bounds.height}; var rb = {x:bounds.width, y:bounds.height}; lt = transformPoint(matrix, lt); rt = transformPoint(matrix, rt); lb = transformPoint(matrix, lb); rb = transformPoint(matrix, rb); var minX = Math.min(lt.x, rt.x, lb.x, rb.x); var minY = Math.min(lt.y, rt.y, lb.y, rb.y); var maxX = Math.max(lt.x, rt.x, lb.x, rb.x); var maxY = Math.max(lt.y, rt.y, lb.y, rb.y); function transformPoint(m, p) { return {x: m.a * p.x + m.c * p.y + m.tx, y: m.b * p.x + m.d * p.y + m.ty}; } return new Rectangle(minX, minY, maxX - minX, maxY - minY); };
这里做了一个变化,如果bounds(也就是边框Rect)有x/y偏移,就把这个偏移转加到Matrix上,把rect简化为(0,0,width,height),这样有利于简化计算。
关键点是transformPoint函数,理解这个线性代数计算就能理解整个2D平面的算法。
其实,由于rect的x、y被简化为0,那么上述算法还可以优化,把函数拆开。最终变成:
p._transformBounds = function(bounds, matrix) { var x = bounds.x, y = bounds.y, width = bounds.width, height = bounds.height; var mtx = new Matrix2D(); mtx.appendMatrix(matrix); if (x || y) { mtx.append(1,0,0,1,x,y); } var x_a = width*mtx.a, x_b = width*mtx.b; var y_c = height*mtx.c, y_d = height*mtx.d; var tx = mtx.tx, ty = mtx.ty; var minX = tx, maxX = tx, minY = ty, maxY = ty; if ((x = x_a + tx) < minX) { minX = x; } else if (x > maxX) { maxX = x; } if ((x = x_a + y_c + tx) < minX) { minX = x; } else if (x > maxX) { maxX = x; } if ((x = y_c + tx) < minX) { minX = x; } else if (x > maxX) { maxX = x; } if ((y = x_b + ty) < minY) { minY = y; } else if (y > maxY) { maxY = y; } if ((y = x_b + y_d + ty) < minY) { minY = y; } else if (y > maxY) { maxY = y; } if ((y = y_d + ty) < minY) { minY = y; } else if (y > maxY) { maxY = y; } return new Rectangle(minX, minY, maxX-minX, maxY-minY); };
两个函数看起来相差很大,但如果大家有心思慢慢计算一下,会发现其实是一样的。
那么,整个计算的过程如下:
p.test = function () { var bounds = new Rectangle(-28, -35, 152, 128); var matrix = new Matrix2D(); matrix.rotate(-60*Math.PI/180); var t = this._transformBounds(bounds, matrix); console.log(t); };
得到
Rectangle {x: -44.31088913245536, y: -124.88715006927039, width: 186.85125168440817, height: 195.6358613752347, initialize: function…}
大功告成。。。
说了一大堆废话,可能大家不理解这种计算意义何在,其实这种边框计算有很多用途,例如脏区重绘、碰撞检测。虽然一般来说,游戏框架都会给你封装好,但在某些情况下,还是不得不自己重新做一遍,这是Kenko在尝试做Flash转Canvas+脏区重绘的工作。
该项目名为Fanvas,现已加入2014年度腾讯6个公司级开源项目,相信不久将来大家会看到这个项目的开源。
【HTML5 Canvas】计算元件/显示对象经过Matrix变换后在上级/舞台上的bounds(边界矩形rect)
标签:
原文地址:http://www.cnblogs.com/kenkofox/p/4445019.html