最短路径算法的实现（dijskstra）：Python

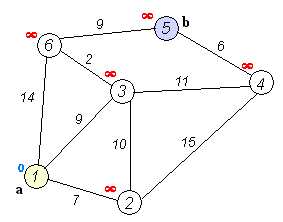
 1 __author__=‘wym‘
 2 #coding=cp936
 3 class Algorithm():
 4     point_list=[]
 5     edge_list=[]
 6     def dijkstra(self,start_point,point_list,edge_list):
 7         ‘‘‘
 8         @point为起始点
 9         @point_list为顶点列表
10         @edge_list为边列表
11         ‘‘‘       
12         #列表点
13         temp_point=[]
14         #起始点，在列表点中的位置
15         point_index=point_list.index(start_point)
16         #初始点到其余各点的距离字典
17         dis_dic=dict()
18         #边列表的首端点列表
19         temp_edge=[]
20         #距离初始化
21         dis_list=[‘inf‘]*len(point_list)
22         temp_point.append(start_point)
23         dis_list[point_index]=0
24         for i in range(len(point_list)):
25             dis_dic.setdefault(point_list[i],dis_list[i])
26         for i in range(len(edge_list)):
27             temp_edge.append(edge_list[i][0])
28         point=start_point
29         #依次遍历加入最小距离的点，并更新原列表中点的距离
30         while len(temp_point)<len(point_list):
31             index=self.find_index(point,temp_edge,edge_list,temp_point)
32             #判断是否走的通
33             if len(index)>0:
34                 value=edge_list[index[0]][2]
35                 add_index=index[0]
36                 for i in index:
37                     if edge_list[i][0] in dis_dic:
38                         dis_dic[edge_list[i][1]]=min(float(edge_list[i][2])+float(dis_dic[point]),float(dis_dic[edge_list[i][1]]))
39                     if value>edge_list[i][2]:
40                         value=edge_list[i][2]
41                         add_index=i
42                 temp_point.append(edge_list[add_index][1])
43                 point=edge_list[add_index][1]
44             else:
45                 point=in_list[in_list.index(point)-1]
46         print dis_dic
47         return dis_dic
48     def find_index(self,point,temp_edge,edge_list,temp_point):
49         ‘‘‘
50         @point:遍历点基准点
51         @temp_edge：边列表的首端点列表
52         @edge_list：边权列表
53         @temp_point：列表点
54         @返回边权列表列表索引
55         ‘‘‘
56         #寻找点的索引，并去除已在列表中的点
57         index=[]
58         for i in range(len(temp_edge)):
59             if point==temp_edge[i] and edge_list[i][1] not in temp_point:
60                 index.append(i)
61         return index
62         
63 if __name__=="__main__":
64     print ‘请输入无向图的顶点‘
65     point_list=input()
66     print ‘请输入无向图的边‘
67     edge_list=list(input())
68     print ‘请输入各边长度‘
69     for i in range(len(edge_list)):
70         print ‘顶点‘+str(edge_list[i][0])+‘顶点‘+str(edge_list[i][1])+‘的长度为：‘
71         length=[input("长度为：")]
72         edge_list[i]+=length
73         edge_list.append([edge_list[i][1],edge_list[i][0],length[0]])
74     while True:
75         print ‘请输入起始点‘
76         start_point=input("start_point=")
77         if start_point in point_list:
78             obj=Algorithm()
79             obj.dijkstra(start_point,point_list,edge_list)
80             break
81         else:
82             print ‘该点不在图中，请重新输入:‘
83             continue